概要
GPyを用いて、サンプルパスの生成、ガウス過程回帰、クラス分類、ポアソン回帰、Bayesian GPLVMを実行しました。自分用のメモです。
参考資料
理論的背景は上記の[3]を参考にしてください。日本語でもガウス過程の解説がMLPシリーズから豪華著者陣で出るようです。超期待しています。
以下のサンプルプログラムは基本的に[2]を元にしています。しかし、古くてそのままでは動かないプログラムや分かりにくいプログラムを少し加工修正しています。なお、環境は以下の通りです。
サンプルパスの生成
RBFカーネルで適当に定めたパラメータの値でサンプルパスを生成するプログラムです。カーネルそのものやカーネルのパラメータを変えることでどのようなサンプルパスを生成するのかシミュレーションしたい場合によく使います。

import GPy
import numpy as np
import matplotlib.pyplot as plt
kernel = GPy.kern.RBF(input_dim=1, variance=1, lengthscale=0.2)
np.random.seed(seed=123)
N_sim = 100
x_sim = np.linspace(-1, 1, N_sim)
x_sim = x_sim[:, None]
mu = np.zeros(N_sim)
cov = kernel.K(x_sim, x_sim)
y_sim = np.random.multivariate_normal(mu, cov, size=20)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
for i in range(20):
ax.plot(x_sim[:], y_sim[i,:])
fig.savefig('output/fig1.png')
- 5行目: これでカーネルを定義します。入力の次元(
input_dim)は必須です。
- 10行目: GPyの関数の多くは、引数の
shapeが(データ点の数, 1)である必要があります。そこで[:, None]を加えてその形にしています。
- 12行目:
kernelオブジェクトに対しK関数を使うと分散共分散行列を作成できます。
- 13行目:
numpyの関数で多変量正規分布からサンプルを生成しています。
ガウス過程回帰(入力1次元・出力1次元)
手順は カーネルを定める→モデル作成→最適化 だけです。

import GPy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
kernel = GPy.kern.RBF(1)
d = pd.read_csv('data-GPbook-Fig2_05.txt')
model = GPy.models.GPRegression(d.X[:, None], d.Y[:, None], kernel=kernel)
model.optimize()
model.plot()
plt.savefig('output/fig2.png')
x_pred = np.linspace(-10, 10, 100)
x_pred = x_pred[:, None]
y_qua_pred = model.predict_quantiles(x_pred, quantiles=(2.5, 50, 97.5))[0]
- 6行目: RBFカーネルを
input_dim = 1で作成しています。7行目はRBF+Bias+Linearのカーネルを使う場合です。足したり掛けたりするだけで複雑なカーネルを作ることができるインターフェースが素敵です。
- 10行目:
GPy.models.GPRegression関数でモデルを作成しています。print(model)やm['']とするとモデルに含まれるパラメータを見ることができます。特に指定しなければ、すべてのパラメータが最適化の対象となります。ちなみに各パラメータに固定値を与えることや制限をかけることができます(詳しくはこれやこれを参照)。
- 11行目: 最適化をしています。オプションでiterationの数などを指定できます。
- 12~13行目: 最適化後のモデルをプロットしています。
- 16~18行目: 最適化後のモデルを使って予測を行っています。
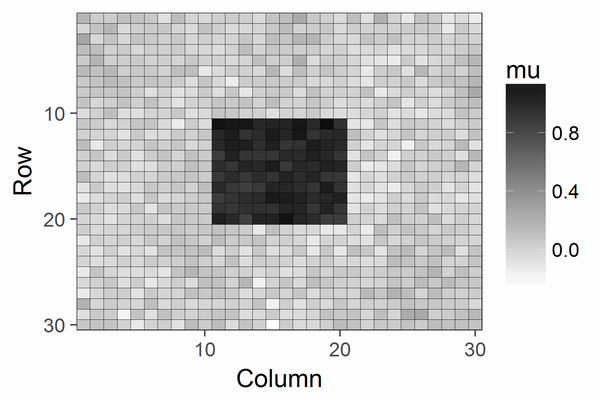
ガウス過程回帰(入力2次元・出力1次元)

import GPy
import numpy as np
import matplotlib.pyplot as plt
kernel = GPy.kern.Matern52(2, ARD=True)
np.random.seed(seed=123)
N = 50
X = np.random.uniform(-3.,3.,(N, 2))
Y = np.sin(X[:,0:1]) * np.sin(X[:,1:2]) + np.random.randn(N,1)*0.05
model = GPy.models.GPRegression(X, Y, kernel)
model.optimize(messages=True, max_iters=1e5)
model.plot()
plt.savefig('output/fig3.png')
model.plot(fixed_inputs=[(0, -1.0)], plot_data=False)
plt.savefig('output/fig3-slice.png')
x_pred = np.array([np.linspace(-3, 3, 100), np.linspace(3, -3, 100)]).T
y_qua_pred = model.predict_quantiles(x_pred, quantiles=(2.5, 50, 97.5))[0]
- 5行目: 今回はMatern5/2カーネルを使っています。オプションの
ARD=Trueは入力の次元1つに対し、1つのlengthscaleパラメータを割り振ること(すなわちGPは等方でないことを表します)。
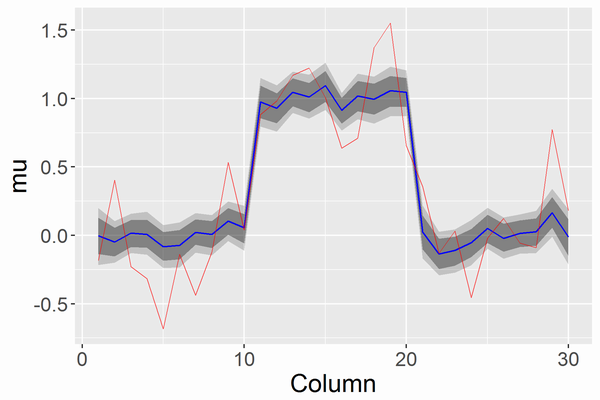
- 17~18行目: 2次元の入力のうち一部を固定した図(スライスした図;2枚目の図)を描いています。ここでは、
fixed_inputs=[(0, -1.0)]でインデックス0の入力を-1.0に固定しています。
- 21~22行目: 入力1次元のガウス過程回帰と同様に予測をしています。入力の次元に注意です。
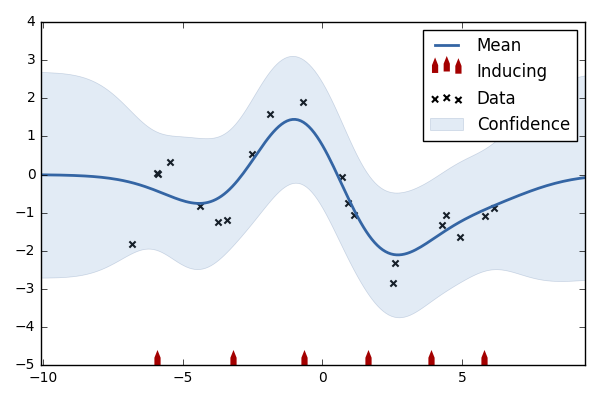
スパースなガウス過程回帰
補助変数法やコンパクトなガウス過程回帰とも呼ばれます。ガウス過程はデータ点の数Nの逆行列を求める必要があり、その部分にN^3のオーダーの時間がかかります。そのため、データ点が増えると次第に遅くなります。そこで、一部の補助変数(inducing inputs)を入力次元の代表点として扱い、対数尤度を近似することで計算を高速化させる方法があります。それがこの節の方法になります。

import GPy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
kernel = GPy.kern.RBF(1)
d = pd.read_csv('data-GPbook-Fig2_05.txt')
m_full = GPy.models.GPRegression(d.X[:, None], d.Y[:, None], kernel=kernel)
m_full.optimize()
Z = np.hstack((np.linspace(-6, -3, 3), np.linspace(3, 6, 3)))[:,None]
m_sparse = GPy.models.SparseGPRegression(d.X[:, None], d.Y[:, None], Z=Z)
m_sparse.optimize()
m_sparse.plot()
plt.savefig('output/fig4.png')
print(m_sparse.log_likelihood(), m_full.log_likelihood())
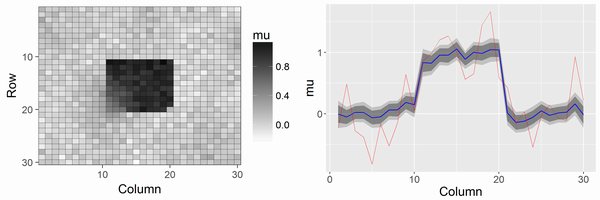
- 12行目: 補助変数の初期値です。6個をテキトーに定めました。結果は1枚目の図です。
- 13行目: こちらは12個の場合です。結果は2枚目の図です。
- 14行目:
GPy.models.SparseGPRegression関数を使います。補助変数はZで指定します。
- 15行目: 補助変数の位置も最適化の対象となります。
- 18行目:
modelオブジェクトに対しlog_likelihood関数を使うと対数尤度を取得できます。最適化の後の対数尤度を見ると、補助変数6個の場合が-28.85、補助変数12個の場合が-18.02、補助変数を使わないフルモデルの場合が-17.92となりました。12個の補助変数で十分よく近似できていることが分かります。
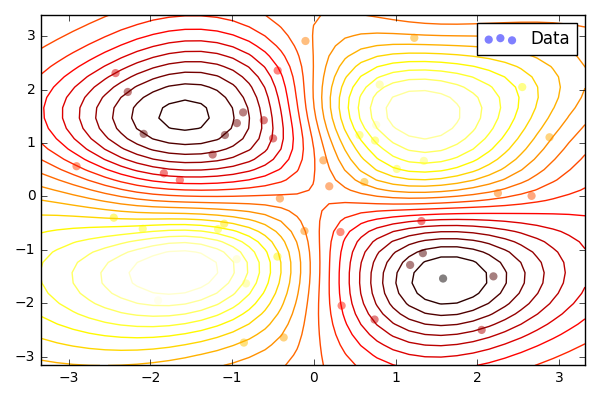
クラス分類
ここではPRML下のFig.6.12相当の図を再現してみます。

import GPy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
kernel = GPy.kern.RBF(2, ARD=True)
d = pd.read_csv('data-classification.txt')
model = GPy.models.GPClassification(d[['X1', 'X2']].values, d.Y[:, None])
model.optimize()
ax = model.plot(plot_data=False)
d0 = d[d.Y == 0]
d1 = d[d.Y == 1]
ax.plot(d0.X1, d0.X2, 'ro')
ax.plot(d1.X1, d1.X2, 'bo')
plt.savefig('output/fig5.png')
- 9行目:
GPy.models.GPClassification関数でクラス分類のモデルを組み立てることができます。
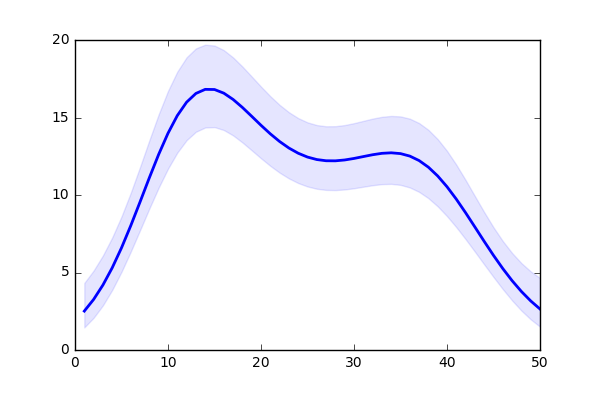
久保緑本の11章の欠測値なしのモデルを実行します。

import GPy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
kernel = GPy.kern.RBF(1)
d = pd.read_csv('data-kubo11a.txt')
model = GPy.core.GP(X=np.linspace(1, 50, 50)[:,None], Y=d.Y[:,None], kernel=kernel,
inference_method=GPy.inference.latent_function_inference.Laplace(),
likelihood=GPy.likelihoods.Poisson())
model.optimize()
model.plot()
plt.savefig('output/fig6.png')
x_pred = np.linspace(1, 50, 50)[:, None]
f_mean, f_var = model._raw_predict(x_pred)
f_upper, f_lower = f_mean + 2*np.sqrt(f_var), f_mean - 2.*np.sqrt(f_var)
plt.plot(x_pred, np.exp(f_mean), color='blue', lw=2)
plt.fill_between(x_pred[:,0], np.exp(f_lower[:,0]), np.exp(f_upper[:,0]), color='blue', alpha=.1)
plt.savefig('output/fig6-mean.png')
- 10~12行目: 少し凝ったモデルを使用したい場合には、
GPy.core.GP関数を使って尤度を自分で設定する必要があります。推定方法もあわせて指定します。ここでは単純なポアソン回帰なので、用意されているGPy.likelihoods.Poisson関数を使えば完了です。
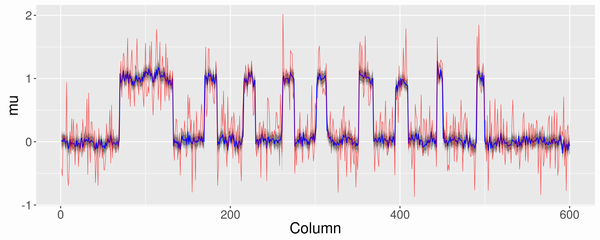
- 17~21行目: 真の平均の推定値と±2SDのグラフ(2枚目の図)を描いています。
ガウス過程回帰(入力2次元・出力2次元)
出力が2次元となると、モデルの選択肢が増えます。その前に「どうして複数次元の出力が必要なのか?各出力は相関しているのか(一方の出力が他方の出力を予測するヒントになるのか)?」といった問いが重要だとNeil Lawrenceは述べています(メーリングリストより)。もしそれらの問いの回答がNoならば、出力1次元のモデルを複数組み合わせたモデルの方がよいかもしれません。
ここでは、「出力間に相関がある簡単なモデル」「出力間に相関がないモデル」「出力間に相関がある凝ったモデル」の順にすすめます。



import GPy
import numpy as np
import matplotlib.pyplot as plt
f_output1 = lambda x: 4*np.cos(x/5) - 0.4*x - 35 + np.random.rand(x.size) * 2
f_output2 = lambda x: 6*np.cos(x/5) + 0.2*x + 35 + np.random.rand(x.size) * 8
np.random.seed(seed=123)
X1 = np.random.rand(100)
X2 = np.random.rand(100)
X1 = X1*75
X2 = X2*70 + 30
Y1 = f_output1(X1)
Y2 = f_output2(X2)
x_pred1 = np.random.rand(100)*100
x_pred2 = np.random.rand(100)*100
y_pred1 = f_output1(x_pred1)
y_pred2 = f_output2(x_pred2)
def plot_2outputs(m):
fig = plt.figure(figsize=(12, 8))
ax1 = fig.add_subplot(211)
ax1.set_ylim([-120, -20])
ax1.set_title('Output 1')
m.plot(plot_limits=[0, 100], fixed_inputs=[(1, 0)], which_data_rows=slice(0, 100), ax=ax1)
ax1.plot(x_pred1, y_pred1, 'rx', mew=1.5)
ax2 = fig.add_subplot(212)
ax2.set_ylim([-20, 100])
ax2.set_title('Output 2')
m.plot(plot_limits=[0, 100], fixed_inputs=[(1, 1)], which_data_rows=slice(100, 200), ax=ax2)
ax2.plot(x_pred2, y_pred2, 'rx', mew=1.5)
K = GPy.kern.Matern32(1)
B = GPy.kern.Coregionalize(input_dim=1, output_dim=2)
kernel = K**B
model = GPy.models.GPCoregionalizedRegression(X_list=[X1[:, None],X2[:, None]], Y_list=[Y1[:, None],Y2[:, None]], kernel=kernel)
model['.*Mat32.var'].constrain_fixed(1)
model.optimize()
plot_2outputs(model)
plt.savefig('output/fig7a.png')
model['.*coregion.W'].constrain_fixed(0)
model.randomize()
model.optimize()
plot_2outputs(model)
plt.savefig('output/fig7b.png')
K1 = GPy.kern.RBF(1)
K2 = GPy.kern.Bias(1) + GPy.kern.Linear(1)
B1 = GPy.kern.Coregionalize(1, output_dim=2)
B2 = GPy.kern.Coregionalize(1, output_dim=2)
kernel = K1**B1 + K2**B2
X = np.vstack((np.concatenate([X1, X2]), np.hstack((np.zeros(100), np.ones(100))))).T
Y = np.hstack((Y1, Y2))[:, None]
model = GPy.models.GPRegression(X, Y, kernel)
model.optimize()
plot_2outputs(model)
plt.savefig('output/fig7c.png')
x_pred = np.arange(100, 110)[:, None]
x_pred = np.hstack([x_pred, np.ones_like(x_pred)])
output_index_pred = {'output_index':x_pred[:,1:].astype(int)}
y_pred = model.predict(x_pred, Y_metadata=output_index_pred)
- 5~19行目: デモデータ作成部分です。
- 21~32行目: プロットする関数を定義しています。
- 36行目: 出力間の関係を定める行列
B(coregionalization matrix)を作成しています。詳しくはここを参照。
- 37行目:
kernelオブジェクトに対する**はクロネッカー積となります。
- 38行目:
GPy.models.GPCoregionalizedRegression関数を使うことで、複数の出力の次元が相関を持ち、出力の各次元でノイズの大きさが異なるモデルを簡単に作成することができます。なお、入力と出力はlistで渡します。
- 40行目: 38行目でもモデルにノイズが入るので、Matern3/2カーネルに含まれるノイズを
1に固定しています。
- 41~43行目: このモデルの結果は1枚目の図です。
- 45行目:
Bを対角行列に固定しています。出力次元ごとにガウス過程回帰を行うのと同じになります。
- 46行目: 41行目で最適化された値になっているので、いったん初期値をぐちゃぐちゃにする意味です。
- 47~49行目: このモデルの結果は2枚目の図です。1枚目の図との違いに注目してください。
- 52~56行目: coregionalization matrixをカーネルの種類ごとに用意して組み合わせることもできます。
- 60行目:
GPy.models.GPRegression関数を使うと、すべての出力次元の共通の大きさのノイズとなります。なお、GPy.models.GPRegression関数を用いる場合にはXは「1列目に値・2列目に出力次元のインデックス」となっているndarrayを渡す必要があります。YはXに対応するndarrayです。
- 61~63行目: このモデルの結果は3枚目の図です。予測区間が狭いです。モデルが複雑で過学習の恐れがあるかもしれません。
- 67~70行目: 予測の例です。出力が複数ある場合には
dictionaryを作って渡します。ここではoutput_indexが1(すなわち2番目の出力)が100~110でどのような出力になるか予測しています。
Bayesian GPLVM
前の記事と同じようにPRMLでおなじみのOil Flowのデータに対してBayesian GPLVMを実行します。

from scipy.io import loadmat
import scipy.io as spio
import GPy
import matplotlib.pyplot as plt
d = spio.loadmat('input/3Class.mat')
X = d['DataTrn']
X -= X.mean(0)
L = d['DataTrnLbls'].nonzero()[1]
input_dim = 2
kernel = GPy.kern.RBF(input_dim, ARD=True) + GPy.kern.Bias(input_dim) + GPy.kern.Linear(input_dim) + GPy.kern.White(input_dim)
model = GPy.models.BayesianGPLVM(X, input_dim, kernel=kernel, num_inducing=30)
model.optimize(messages=True, max_iters=5e3)
model.plot_latent(labels=L)
plt.savefig('output/fig8.png')
- 10行目: 潜在変数の次元。ここではチュートリアルと同じように
2にしています。
- 13行目:
GPy.models.BayesianGPLVM関数の一発で補助変数込みでモデルが作成できます。
不明点
GPy.models.GPRegression関数を使うと、パラメータにノイズの大きさが加わります。このノイズと、カーネル側でGPy.kern.White関数で設定したノイズの違いがよく分かりません。なお、簡単なモデルで両方とも設定すると数式の上では識別できなくなると思うのですが、最適化の結果は分散をちょうど半分に分ける形で推定されて全体的な予測分布は変わりません。
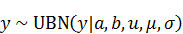
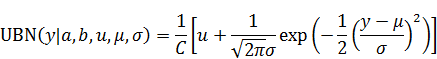
]の範囲の値を生成する、切断正規分布に一様分布のゲタをはかせたような分布です。ここで、
は一様分布の範囲を決めるパラメータ、
は一様分布のゲタの高さを決めるパラメータ、
は正規分布の平均と標準偏差、
は正規化項です。この分布は一様分布と切断正規分布の混合分布なのですが、ベルヌーイ分布とポアソン分布の混合分布をZero-inflated Poisson分布と分かりやすく呼ぶのになぞらえて、この記事では上記の分布をUniformly Boosted Normal Distributionと呼び、以下では略してUBN分布と呼びます。思いつけばコロンブスの卵ですが、UBN分布はコーシー分布の利点である裾の長さを保ったまま、サンプリングの非効率さを解消します。例えば、
,
,
,
,
の場合には
はほぼ2となり、以下のような確率密度になります。
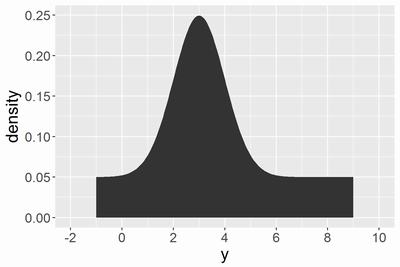
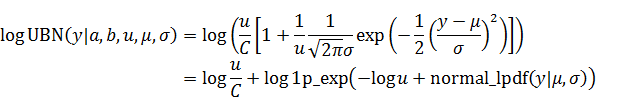
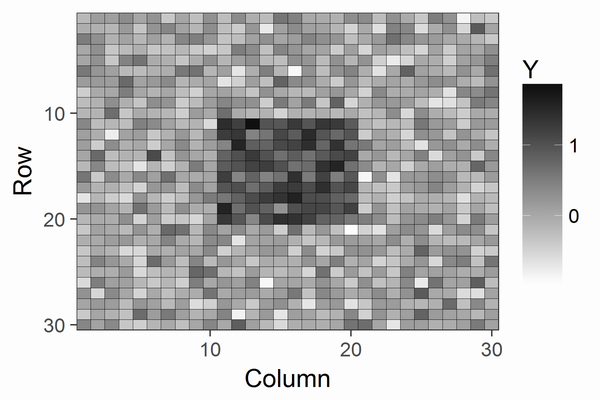
を固定値
と
にそれぞれ対応しています。
はほぼ一定の定数です。Stanでは対数確率の偏微分が重要であり、微分で消える定数項を無視して構いません。そのため
を無視してコーディングしています。