逆温度1の事後分布のサンプルからWBICを計算する

この記事は以下のツイートを拝見してやってみようと思いました。

#統計 #Baysian もしも「元論文の式(20)をβ₁=1, β₂=1/log nの場合に適用した公式を使ってWBICを計算すると事後分布のサンプルの違いによる分散が大きくなる」とか「直接逆温度1/log nの事後分布のサンプルを生成して計算した方が精度が高い」とかの情報を知っている人がいたら教えて下さい。

— 黒木玄 Gen Kuroki (@genkuroki) 2017年11月10日

ツイートで言及されている渡辺先生の論文は以下です。

• S Watanabe (2013) "A widely applicable Bayesian information criterion" Journal of Machine Learning Research 14 (Mar), 867-897 (pdf file)

この記事では、以前WAICとLOOCVの比較をした時に使った3つのモデル（重回帰、ロジスティック回帰、非線形回帰）において、「定義通りに算出したオリジナルのWBIC」と「近似式（上記論文の(20)式）で求めたWBIC」を比較してみました。

手法

case 1 重回帰

真のモデルは以下です。

　

あてはめたモデルは以下です。

　

データ点の数Nについては20,100を試しました。例としてN = 20の場合を説明します。まず乱数でデータX（すなわち）を生成します。次にそのXの値を使ってYを生成しますが、以下の二つの場合について計算しました。

• 1) MCMCサンプルの出方の違いによる影響: Yを1つだけ生成して固定し、MCMCの乱数の種を変えて200回推定を行い、・のそれぞれの分布を確認した
• 2) データの出方の違いによる影響: Yを1000通り生成し、および相対的な差であるの分布を確認した

事後分布の推定はStanで行いました。iter=11000, warmup=1000, chains=4で実行して合計40000個のMCMCサンプルを得ています。

case 2 ロジスティック回帰

手順は重回帰の場合と同じです。使用したモデルだけが異なります。真のモデルは以下です。

　

あてはめたモデルは以下です。

　

　

case 3 非線形回帰 ミカエリス・メンテン型

手順は重回帰の場合と同じです。使用したモデルだけが異なります。真のモデルは以下です。

　

あてはめたモデルは以下です。

　

　

　

case 3b 真のモデルが含まれない場合

あてはめたモデルが以下の場合も試しました。

　

結果

計算速度

Stanを使う場合、近似式のモデルの方がサンプリングが速いので、計算速度は近似式の方が少し速いです。どれだけ速くなるかはモデル依存で場合によりけりです。

MCMCサンプルの出方の違いによる影響

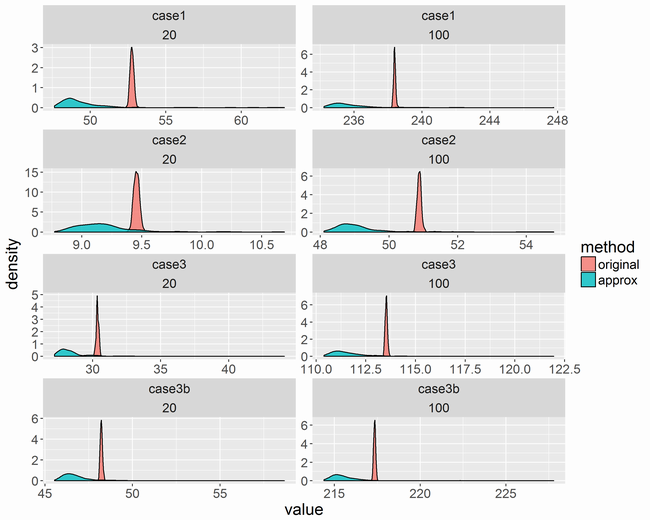
近似式の方はMCMCサンプルの出方によってかなりばらつくようです。また、少し値が低くなっています。

データの出方の違いによる影響

差

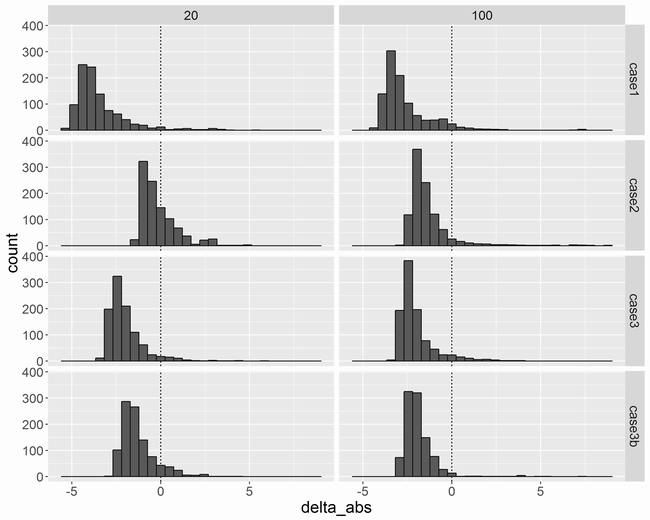
横軸はです。少しマイナスに偏った分布になりました。これが近似で捨てた項の影響なのか、Stanによるサンプリングの影響なのかは分かりません。

相対的な差

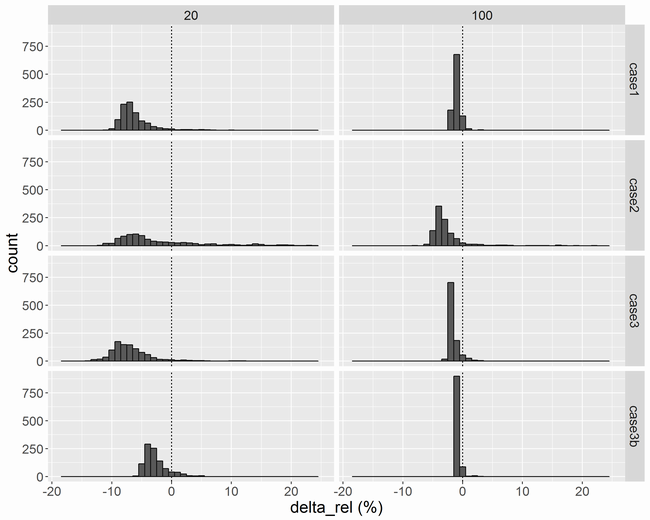
横軸は相対的な差であるです。ロジスティック回帰のN = 20の場合は、しばしばが0に近くなるので尾を引いています。Nが増えるに従って相対的な差は小さくなり、N = 100では±5%ぐらいに収まりそうです。

まとめ

Nが大きいときは近似式でスピードを重視しても大丈夫そう。でもNが小さいときは定義通り計算した方が無難に思えます。

ソースコード

case 1のソースコードを以下に載せます。

オリジナルのWBICを算出するためのStanコード

model/model1-ori.stanというファイル名とします。

data {
  int D;
  int N;
  matrix[N,D] X;
  vector[N] Y;
}

parameters {
  vector[D] b;
  real<lower=0> sigma;
}

transformed parameters {
  vector[N] mu;
  mu = X*b;
}

model {
  target += 1/log(N) * normal_lpdf(Y | mu, sigma);
}

generated quantities {
  vector[N] log_lik;
  for (n in 1:N)
    log_lik[n] = normal_lpdf(Y[n] | mu[n], sigma);
}

近似式でWBICを算出するためのStanコード

model/model1-apx.stanというファイル名とします。

data {
  int D;
  int N;
  matrix[N,D] X;
  vector[N] Y;
}

parameters {
  vector[D] b;
  real<lower=0> sigma;
}

transformed parameters {
  vector[N] mu;
  mu = X*b;
}

model {
  Y ~ normal(mu, sigma);
}

generated quantities {
  vector[N] log_lik;
  for (n in 1:N)
    log_lik[n] = normal_lpdf(Y[n] | mu[n], sigma);
}

各WBICを算出するRコード

library(rstan)

wbic_original <- function(log_lik) {
  wbic <- - mean(rowSums(log_lik))
  return(wbic)
}

wbic_approx <- function(log_lik) {
  b2 <- 1.0/log(ncol(log_lik))
  b1 <- 1.0
  log_denominator <- statnet.common::log_sum_exp(-(b2-b1)*(rowSums(-log_lik)))
  log_numerator   <- statnet.common::log_sum_exp(-(b2-b1)*(rowSums(-log_lik)) + log(rowSums(-log_lik)))
  wbic <- exp(log_numerator - log_denominator)
  return(wbic)
}

set.seed(123)
D <- 3
b <- c(1.3, -3.1, 0.7)
SD <- 2.5
N <- 100

X <- cbind(1, matrix(runif(N*(D-1), -3, 3), N, (D-1)))
Mu <- X %*% b
Y <- rnorm(N, Mu, SD)
data <- list(N=N, D=D, X=X, Y=Y)

sm_ori <- stan_model(file='model/model1-ori.stan')
sm_apx <- stan_model(file='model/model1-apx.stan')
fit_ori <- sampling(sm_ori, pars='log_lik', data=data, iter=11000, warmup=1000, seed=123)
fit_apx <- sampling(sm_apx, pars='log_lik', data=data, iter=11000, warmup=1000, seed=123)
wbic_ori <- wbic_original(rstan::extract(fit_ori)$log_lik)
wbic_apx <- wbic_approx(rstan::extract(fit_apx)$log_lik)
c(wbic_ori=wbic_ori, wbic_apx=wbic_apx)

• 3～6行目: を算出します。この記事参照。
• 8～15行目: を算出します。途中で{statnet.common}パッケージのlog_sum_exp関数を使っています。前の記事のようにStanに含まれるlog_sum_exp関数を使っても構いません（全く同じ数値になります）。
• 9行目: log_likはN_mcmc×N（データの数）のmatrix型ですのでncol(log_lik)でNを取得しています。

渡辺先生の論文の(20)式の通りに計算しようとすると、expの内側が50ぐらい以上の数値になるため、計算が不安定になります。そのため(20)式の両辺の対数をとって計算して、最後にexpをかませて戻します。MCMCを使っている場合、(20)式の左辺の対数は以下のように式変形できます。

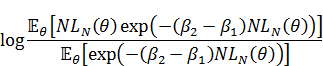
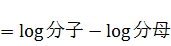
なので、まず易しい分母の方から計算すると、

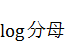
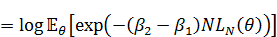
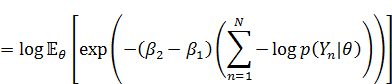
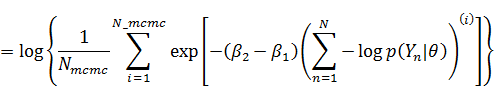
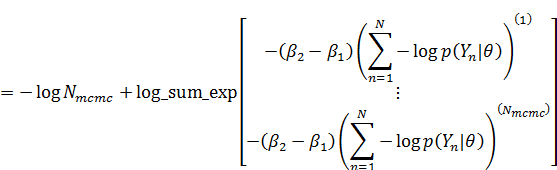
分子の方も同様に、

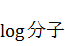
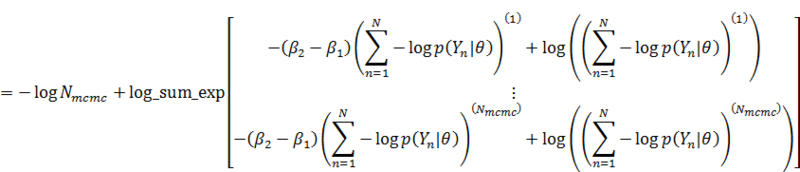
これをそのまま実装しています。

Enjoy!

Stanの関数を使ってRを拡張して高速化する

（C++に自動で変換される）Stanの関数を使ってRを拡張できる機能が、Stan/RStanの2.16で実装開始されて2.17でほぼ完成しました。Rを高速化するためにC++（とRcpp）はあまり書きたくないけれど、Stanの関数なら書いてもいいよという僕得な機能です。この記事ではその方法を簡単に紹介します。

元にした資料はRStanの開発者であるBenさんがStanCon2018で発表したこちらの資料です。

ここでは例として、以下の2つの関数をRで使えるようにしましょう。

• 1) 機械学習分野でおなじみのlog_sum_exp関数
  • 引数はN個の正の実数
• 2) データにemax modelという曲線をあてはめた場合の対数尤度を返す関数
  • 引数はデータ（N個のXとYのペア）とパラメータの値

手順は簡単で以下だけです。

• functionsブロックだけ書いたstanファイルを用意する
• R側でrstan::expose_stan_functions()を呼び出す

具体的には、以下の内容を例えばmy_functions.stanという名前で保存します。

functions {
  real stan_log_sum_exp(vector x) {
    return(log_sum_exp(x));
  }

  real emax_model_ll(vector Y, vector X, real e0, real emax, real ed50, real sigma) {
    int N = num_elements(Y);
    vector[N] mu = e0 + emax*X ./ (ed50 + X);
    real ll = normal_lpdf(Y | mu, sigma);
    return(ll);
  }
}

• 3行目：log_sum_exp関数の方はすでにStanに用意されているものを使います。
• 6行目：接尾の_llはlog likelihoodの意味です。
• 7行目：たしかStan 2.14ぐらいから変数の宣言と定義を同時にできるようになりました。ここではデータポイントの数NをYから動的に取得しています。

次にR側でrstan::expose_stan_functions()を呼び出します。

rstan::expose_stan_functions('my_functions.stan')

するとfunctionsブロックに入っていた関数は全てR側で使えるようになります。

stan_log_sum_exp(c(0.1, 0.05, 0.8))
emax_model_ll(Y=c(1,10,12,24), X=c(0,5,10,10), e0=0.8, emax=30, ed50=5.1, sigma=3)

StanのコードはC++のコードに変換されるのでfor文はRと比べて非常に高速です。また、Stanのマニュアル（特にBuilt-In Functionsの章以降）を見ていただくとよいのですが、Stanはマニアックな分布の対数尤度を求める関数や、行列演算の関数（Eigen由来）や、log1m_expなどの指数対数を安定に計算する関数が豊富です。

これらのStanの長所を非常に簡単にRのコーディングに取り込めるのは最高です。まあ、少しばかりStanの関数やデータ型に慣れている必要がありますが。

Enjoy!

IGMRFの尤度におけるrankの減少分に関するメモ

以下の書籍を読んで、IGMRF（Intrinsic Gaussian Markov Ramdom Field）の尤度に関して自分の理解をまとめたメモです。

[asin:B00YBV6YLI:detail]

この発表資料の18ページにおいて、（観測モデル部分を除いた）IGMRFの対数尤度は以下に比例すると書きました（ただしをに、をに読み替えてください）。

ここではnodeの数、はの精度行列*1でnodeのつながりの情報を反映していて、は線形制約に由来するのrankの減少分です。

1次元の1階階差のIGMRF

線状につながれたGMRFの場合、は以下になります。

このように精度行列が帯行列になってスパースになるところがGMRFの特徴です（分散共分散行列はスパースにならない）。

ここで、という線形の制約を満たすことに注意してください。に定数を足して平行移動しても、の要素の差しか尤度に関わってこないので、全体の尤度は不変であることがこの制約の由来です。数式で表現すると、をに平行移動しても、はと同じになります。を位置のインデックスとしてをに変えても同じという意味です。という制約のため、のrankは1だけ減少して、となります。よって、IGMRFの対数尤度は以下になります。

1次元の2階階差のIGMRF

線状につながれたGMRFの場合、は以下になります。

ここで、という制約を満たします。 は以下の行列です。

これはに直線を足しても差の差（例：）しか尤度に関わってこないので、直線の傾きがキャンセルされて全体の尤度は不変であることがこの制約の由来です。数式で表現すると、をに変えても、はと同じになります。ここでです。を位置のインデックスとしてをに変えても同じという意味です。という制約のため、のrankは2だけ減少してになります。よって、IGMRFの対数尤度は以下になります。

次元の階階差のIGMRF

次元の階階差のGMRFではrankはいくつになるでしょうか。結論を先に書くと、以下になります。

ここで、はnodeの数です。そこから二項係数を引いています。ここで、をすべてのnodeを1列に並べたベクトルとします。すると、をに変えても尤度は不変となります。このの列の数（＝の要素数）がrankの減少分に相当します。これまでの例ではは、だったり、だったりしました。これまでの例と同じように、 に加えても不変になる項を求めると以下になります。

ここから、の要素数は次のように数えます。の添字の数が個で、各添字の数値の範囲が～で、添字の数値の合計は以下となる制限があります。この状況は、部屋の仕切り個と個の玉の並び替えの場合の数と同じになるので、の要素数は以下になります。

例えば2次元3階階差の場合、 に加えても不変になる項は、以下になります。

　

の要素数は6個になりますので、rankの減少分は6になります。例えば、は、以下の部屋の仕切りと玉の図に相当します。

Stanによる実装例

「StanとRでベイズ統計モデリング」の12.8節の例題（2次元1階階差の地図）のStanコードは以下になります。

data {
  int N;
  vector[N] Y;
  int I;
  int<lower=1, upper=N> From[I];
  int<lower=1, upper=N> To[I];
}

parameters {
  vector[N] r;
  real<lower=0> s_r;
  real<lower=0> s_Y;
}

model {
  target += - (N-1) * log(s_r) - 0.5 * dot_self(r[To] - r[From]) * inv_square(s_r);
  Y ~ normal(r, s_Y);
}

なお、先にを頑張って構築してquad_formなどを利用してモデルを書く方法は、上記のように書く方法より遅くなりました。ベクトル化がうまく効かないからだと思います。なお、12.8節のモデルと比べるとの部分は等価ですが、外側のlog(s_r)に掛かる定数が異なります（12.8節のモデルがよりが小さくなる方へペナルティが入っています）。

*1:厳密にはrankが落ちているので精度行列そのものとは言えませんが、ここでは[4]にならって区別しないでそう呼びます。