この記事では階層ベイズモデルの場合のWAICとは何か、またその場合のWAICの高速な算出方法について書きます。
背景
以下の2つの資料を参照してください。[1]に二種類の実装が載っています。[2]に明快な理論的補足が載っています。
- [1] 階層ベイズとWAIC (清水先生の資料です、slideshare)
- [2] 階層ベイズ法とWAIC (渡辺先生の資料です、pdf, html)
モデル1
資料[1]にあるモデルを扱います。すなわち、
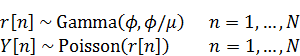
ここでは人数、
は人のインデックスです。
は個人差を表す値になります。このモデルにおいては
を解析的に積分消去することができて、負の二項分布を使う以下のモデル式と等価になります。

ここでは予測として(WAICとして)2通り考えてみましょう。
以降では事後分布による平均を、分散を
と書くことにします。
(1) ![r[n]](https://chart.apis.google.com/chart?cht=tx&chl=%20r%5Bn%5D%20) を持つ
を持つ が、追加で新しく1つのサンプルを得る場合
が、追加で新しく1つのサンプルを得る場合
この場合には新しいデータの予測分布は以下になります。

WAICはごとに算出され、以下になります。

(2) 別の新しい人が新しく1つのサンプルを得る場合
この場合には次のモデルを考えていることに相当します。
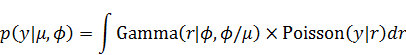
そして、新しいデータの予測分布は以下になります。

WAICは以下になります。
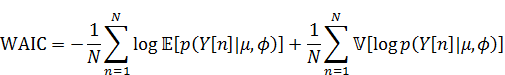
ソースコード
ごとにWAICを算出することや、WAIC内の和(シグマ)はR側で処理します。
(1)のStanコード
(2)に対応する負の二項分布を使ったStanコード
(2)のStanコード
数値積分をR側かStan側のどちらかで実行する必要があります。資料[1]ではR側で行っており、これが多大な時間がかかる原因となっています。ここでは合成シンプソン公式(とlog_sum_exp関数)を使ってStan側で数値積分をして高速化します。
これはこちらのコードをメモ化によって高速化したものになっています。どちらのコードでも6~17行目でシンプソンの公式を使って数値積分をしています。
Rコード
結果
waic1_byG |
waic2 |
waic3 |
|---|---|---|
| 2.332 3.244 2.841 ... 2.987 | 3.14 | 3.143 |
計算時間は(1)の場合は、Surface Pro 3で1chainあたり5秒ぐらいです。(3)の場合でもメモ化がバッチリ効いて1chainあたり12秒ぐらいです。
waic1_byGにおいて、r[n]の大きなnはr[n]の小さなnと比べて、ガンマ分布の裾部分の確率密度に由来する可能性が高く、(1)の予測が悪くなる(WAICが大きくなる)ことが予想されるでしょう。ここでは図示しませんが調べるとそうなっています。
waic2とwaic3は理論的に一致するはずですが、Stanコードの違いがMCMCサンプルの違いになり、その影響でわずかにズレます。
なお、資料[1]のp.47-48のソースコードだと(1)の場合のWAICをごとに算出したあとに、それらの和をとって
で割った値になります。WAICの和は「各
が、追加でそれぞれ新しく1つのサンプルを得る場合」の予測に対応します。それを
で割った値が対応する予測はよく分かりません。
また、WAICはMCMCサンプルによって値が変わるので、乱数の種の影響をわずかにうけることに注意です。
モデル2
資料[2]にあるモデルと似たモデルを扱います。すなわち、
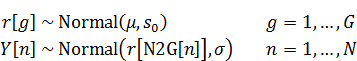
ここではクラス数(グループ数)、
はそのインデックスです。
は人数、
はそのインデックスです。
は
が所属している
を返します。
ここでは予測として(WAICとして)3通り考えてみましょう。
(1) あるクラス に、新しく1人が加わる場合
に、新しく1人が加わる場合
この場合には新しいデータの予測分布は以下になります。

WAICはごとに算出され、以下になります。
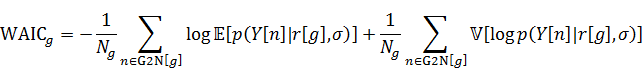
ここではクラス
に含まれる
のインデックスすべてです。
(2) 別の新しいクラスがまるごとできる場合
この場合には新しいクラス全体のデータの予測分布は以下になります。

の記法は資料[2]を参照してください。
WAICは以下になります。
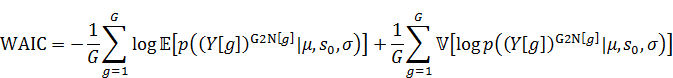
(3) 別の新しいクラスができて、新しく1人が加わる場合
この場合には新しいデータの予測分布は以下になります。

WAICは以下になります。
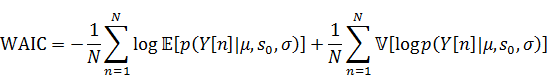
ソースコード
(1)のStanコード
(2)のStanコード
グループ差や個人差が正規分布から生成される場合には、-5SDから+5SDぐらいまでを数値積分すればかなりよい近似になります。
(3)のStanコード
これはこちらのコードをYによって変わらない部分をはじめに計算して保持しておいて、Yによって変わる部分だけをループで計算することで高速化したものになっています。
Rコード
結果
waic1_byG |
waic2 |
waic3 |
|---|---|---|
| 2.537 2.390 2.750 ... 2.496 | 142.1 | 3.679 |
計算時間は(1)(2)(3)の場合がそれぞれ、1chainあたり0.4秒・1秒・12秒ぐらいです。こちらはメモ化ほど高速化が効きませんが、それでも高速化しない場合と比べると1.5倍ぐらい早くなっています。
waic1_byGにおいて、クラスあたりの人数(NbyG)の多いクラスの方がWAICは小さくなるかなと思ったのですが、そこまできれいな関係ではありませんでした。ただし、人数が5人のクラスはWAICは目に見えて高くなっています。











![プログラミングコンテストチャレンジブック [第2版] ~問題解決のアルゴリズム活用力とコーディングテクニックを鍛える~ プログラミングコンテストチャレンジブック [第2版] ~問題解決のアルゴリズム活用力とコーディングテクニックを鍛える~](https://m.media-amazon.com/images/I/41bHxtpurqL._SL160_.jpg)

