StatModeling Memorandum

StatModeling Memorandum

StanとRとPythonでベイズ統計モデリングします. たまに書評.

「StanとRでベイズ統計モデリング」松浦健太郎 という本を書きました

Stan 書評

僕が筆者なので、この記事は書評ではなく紹介になります。まずこの本はRのシリーズの一冊にもかかわらずStanという統計モデリングのためのプログラミング言語の方がメインです。このようなわがままを許してくれた、ゆるいふところの深い石田先生と共立出版には感謝しかありません。

StanとRでベイズ統計モデリング (Wonderful R)

StanとRでベイズ統計モデリング (Wonderful R)

目次と概要

共立出版のページを見てください。GitHubのリポジトリもあります。

前提とする知識

「はじめに」の部分で触れていますが、確率と統計の基本的な知識はある方、R（やPython）で簡単なデータ加工や作図が一通りできる方を想定しています。そのため、確率分布なんて聞いたことがない、プログラミングがはじめて、Rがはじめて、という方が読み進めるのは厳しいかもしれません。なお、Rの基本的な関数しか出てこないので、PyStanとmatplotlib（あるいはSeabornなど）でやるわっていうPythonユーザの方にも十分に読む価値があると思います。

Pythonユーザのための追記

この本を読んで習得できるもの

「統計モデリングの考え方」と「Stanの使い方」の二点です。

統計モデリングの考え方

基本的にデータ解析には「正解」がありません。検定の前提条件にせよ、統計モデルにせよ、機械学習のモデルにせよ、すべてのモデルは仮定にすぎないからです。しかし、ルール無用ではありません。得られた結果が有用であるため、統計モデリングにも沿うべき指針や考え方があります。統計モデリングは従来の検定ベースの統計と比べると、得意分野も考え方も大きく異なります。筆者は仕事がら普段は検定も使っていますが、「ある現象を理解したい・知識を獲得したい・予測したい」といったデータ解析の主目的については、検定では満足できない場合が多いです。その場合、統計モデリングがよい選択肢になります。この本では統計モデリングをきちんと習得できるように、考え方や手順といった正解がないものについても大胆に筆者の主張を書きました。

Stanの使い方

最近Stanを取り上げたデータ解析の本は増えてきています。僕が確認している範囲だけでも以下があります（刊行順）。

しかし、これらの多くは重回帰のような簡単な解析を数ページで紹介しているだけだったり、Stanの文法などは付録だったりしました。「Stanをしっかり学びたい。より美しく、より速く動くように書きたい。」という人にとって十分に満足できる本はこれまでなかったと言えます。しかし、本書はこのニーズにほぼ100%応えた、日本語で読めるはじめての本格的なStan解説書です。

このブログとの関係

いくつかの記事については本の後半の例題とオーバーラップがありますが、基本的には書き下ろしです。本では用語の説明や結果の解釈などの基礎から順番に説明しています。このブログは僕のメモを兼ねているのでやや難しい題材やStanコードが多いですが、本ではそんなことありません。

その他の特徴

例題からはじまる

なるべく具体的なイメージをもって分かりやすくなるように、多くの解説は例題データの解析からはじまります。

図が多い

統計モデリングを含むデータ解析は可視化と密接に関係しているので、図をふんだんに載せています。図と作図のRコードもGitHubにほぼすべてありますので、よろしければ見てください。ただし、作図は各自が好きなパッケージを使えばよいと思っているので作図のRコードの解説は割愛しました。すみません。

数式は難しくない

ベイズ統計の本では1ページまるまる難解な式変形という本も少なくないです。しかし、この本はソースコードとその解説が多めですが、数式は少なめです。式変形も理系の大学一二年生なら引っかかることなく追うことができるでしょう。

Stanの最新版に対応していく

書籍は2.11対応ですが現時点の2.15にもほぼ対応しています。今後もバージョンアップしたら、GitHub上でどの記述が古くなったか書きます。またソースコード自体もアップデートする予定です。

他人からの書評や感想 (追記)

献本勢が多いので褒める言葉は話半分でよいと思いますが、他人から見てよかった章の紹介などは参考になると思います。

この他にも色々コメントいただいております。ありがとうございます。

読書会・勉強会

読書会が開かれることになりました。大変ありがたいです。

なお、愛称は「アヒル本」になった模様です（表紙のブロックはアヒルなのです）。

各章の紹介

以下では実物を手に取って見ることができない人のために、どんなことが書かれているか簡単に紹介したいと思います。

はじめに

本書のあらすじが載っています。

f:id:StatModeling:20201106183153p:plain

1～3章は理論編です。数式が多いわけではなく用語の確認の意味合いが強いです。4～5章はStanの入門編です。6章以降は発展編です。6・8・11・12章が本流で、モデルのレパートリーを増やす章になっています。対して、7・9・10章はモデルを改善する章となっています。特に発展編では読者はStanの強力さを実感できると思います。

1章 統計モデリングとStanの概要

「統計モデリングとは何なのか？目的は？メリットは？」という点について筆者なりの考えを述べました。またStanなどの確率的プログラミング言語を使うメリットを簡潔に説明しています。一部抜粋します。

確率的プログラミング言語とは「様々な確率分布の関数や尤度の計算に特化した関数が豊富に用意されており、確率モデルをデータにあてはめることを主な目的としたプログラミング言語」である。ユーザーはモデルをプログラミングコードで記述し、データを渡すだけでよい。すると確率的プログラミング言語の方でほぼ自動的にパラメータの値を推定してくれる。このようにモデルの記述と難しい推定計算を分離することによって、モデルの可読性が上がり、バグの混入が激減し、解析者はモデルの試行錯誤に専念できるようになる。特に多数のモデルを試行錯誤する状況で確率的プログラミング言語は真価を発揮するのである。

2章 ベイズ推定の復習

確率分布や「 y \sim Poisson(\lambda)」などの基本的な用語や記法の確認からはじまります。そのあとでベイズ統計とMCMCに関する用語を簡潔に説明しました。扱った用語は以下の通りです。

3章 統計モデリングをはじめる前に

まず一般にデータ解析に必要となる前準備について説明しています。そのあとで統計モデリングの手順を筆者なりに以下のように定型化しました。

  • 解析の目的
  • データの分布の確認
  • メカニズムの想像
  • モデル式の記述
  • Rでシミュレーション
  • Stanで実装
  • 推定結果の解釈
  • 図によるモデルのチェック

本書の以降の例題はなるべくこの手順に沿って解析をすすめています。もちろん、現実のデータ解析はこの手順に尽きているわけではなく、あくまでも最低限踏むべきステップの目安です。また、事前知識の役割や、誤解の多いモデルの「正しさ」についても少し触れました。

4章 StanとRStanをはじめよう

インストール方法、基本的な文法、targetとlp__を説明した後で、じっくり単回帰の問題を扱います。この章以降ではStanコード・Rコードとそれらの説明という部分が多くなります。推定結果の見方、収束の判断、trace plotの見方、{ggmcmc}パッケージの使い方、MCMC設定の変更、MCMCサンプルの使い方を説明しています。

5章 基本的な回帰とモデルのチェック

重回帰・二項ロジスティック回帰・ロジスティック回帰・ポアソン回帰を扱います。また図によるモデルのチェック方法を数通り紹介しています。使用した図をいくつか載せておきます。詳しくは本を読んでください。

f:id:StatModeling:20201106183157p:plain

f:id:StatModeling:20201106183201p:plain

f:id:StatModeling:20201106183206p:plain

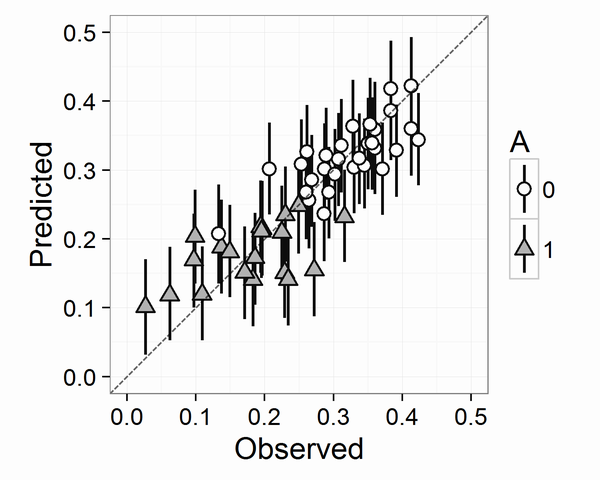
6章 統計モデリングの視点から確率分布の紹介

確率分布の軽い紹介はどんな本にも載っていて、常々冗長だ退屈だと感じていました。しかし、統計モデリングにおいて個々の確率分布は必要不可欠なパーツです。そこで、従来の本にはないような「統計モデリングの視点から」の部分になるべく注力して16個の確率分布を紹介しました。

7章 回帰分析の悩みどころ

交互作用、対数をとるか否か、非線形の関係、打ち切り、外れ値など、ふつうの統計の教科書にはあまり載っていませんが、実際のデータ解析では必ずといっていいほど直面する悩みどころを取り上げました。

8章 階層モデル

階層モデルはグループ差や個人差をうまく扱うための一手法です。ゆっくり導入をした後で応用方法になじめるように、複数の階層を持つ場合や、非線形モデルやロジスティック回帰の階層モデルを取り上げました。

9章 一歩進んだ文法

Stanをより美しく、より速く動くように必要な一歩進んだ文法を解説しました。Stanで用意されている型（かた）の説明やベクトル化、行列演算、パラメータの制約、欠測値がある場合などを扱っています。

10章 収束しない場合の対処法

統計モデリングの最大の難所は、MCMCが収束しないことだと言っても過言ではありません。しかしながら、その対策を系統的に扱った書籍や情報はあまりありません。ここではその対策を大きく4つの節に分けて説明しています。個人的な経験からは、10.1節の識別性の問題（多重共線性を含む）と10.2節の弱情報事前分布で収束しない場合の8割は解決できそうです。

11章 離散値をとるパラメータを使う

Stanの最大の弱点は離散値をとるパラメータが直接的に使えないことです。この章では、log_sum_exp関数と周辺化消去（marginalizing out, summing out）で解決する方法を説明します。応用例として、混合正規分布、ゼロ過剰ポアソン分布、Latent Dirichlet Allocationを扱います。変分ベイズ法の一実装であるADVIも使ってみます。

12章 時間や空間を扱うモデル

時系列データを解析するにあたり、応用範囲が広く、解釈がしやすく、拡張性が高い「状態空間モデル」を取り上げました。特に日次の売り上げデータのように、時刻が離散的で等間隔なデータの場合に使いやすいモデルです。季節調整項や変化点検出なども扱います。後半では、時間構造と空間構造の等価性を説明し、マルコフ場モデル（CARモデルとほぼ同じもの）を使った例題を扱っています。