infer.netの例題シリーズ1 Bayes Point Machine

BayesPointMachine（以下BPM）の元論文はこちら（R.Herbrich, T.Graepel, and C.Campbell, BayesPointMachines, JMLR, 2001）。

BPMはクラス分類を行うアルゴリズムでSVMに似ています。SVMはマージンを最大にするwを求めますが、BayesPointMachineはモデルの尤度に応じたwの分布を求めます。あるクラスに属する確率の分布も求まります。

対応するinfer.netのページはこちら。例題で与えられたデータを以下のようなテーブルにしました。

Y	income	age
1	63	38
0	16	23
1	28	40
1	55	27
0	22	18
0	20	40
NA	58	36
NA	18	24
NA	22	37

ここで、Yは購入したか否かを表すクラス、incomeは収入、ageは年齢です。incomeとageからYを予測せよ、という問題です。最初の6人がTrainingデータ、最後の3人はTestデータです。今回はinfer.netのサンプルコードに忠実に線形判別のモデル（SVMで線形カーネルを用いた場合に相当）をBUGSで実装しました。

BUGSコードは以下になります。たった10行です。

model {
   for (i in 1:N) {
      Y[i] ~ dbern(p[i])
      p[i] <- phi(x[i])
      x[i] ~ dnorm(mu[i], 10)
      mu[i] <- inprod(w[], Personal[i,])
   }
   w[1:N.w] ~ dmnorm(Zero[], tau[,])
   tau[1:N.w, 1:N.w] ~ dwish(R[,], N.w)
}

• 3-4行目: infer.netでは不等号で0,1に変換していますが、BUGSではlogit()やphi()を使うのが安定です。step()とか使うと制限がきつすぎるためか収束しません。
• 8-9行目: infer.netのコードに習ってwの事前分布を多変量正規分布にしています。逆ウィシャート分布（dwish）の自由度パラメータはデータの次元以上である制限があります。値が低いほど無情報です。収束しない場合は値を増やしてもいいかもしれません。flyioさんの大変ためになるブログ記事を参照。

実行するRコードは以下のようになります。

source("R2WBwrapper.R")
d <- read.delim("input/data.txt", as.is=T, header=T, sep="\t")
N <- nrow(d)
Personal.m <- as.matrix(cbind(scale(d[,-1]), Intercept=rep(1, length=N)))
N.w <- ncol(Personal.m)

clear.data.param()
set.data("N", N)
set.data("Y", d$Y)
set.data("N.w", N.w)
set.data("Zero", rep(0, N.w))
set.data("R", diag(rep(0.5, N.w), N.w))
set.data("Personal", Personal.m)

set.param("x", d$Y-0.5, save=F)
set.param("w", rep(0, N.w))
set.param("tau", diag(rep(10, N.w), N.w))
set.param("p", NA)

post.bugs <- call.bugs(
   file = "model/model.bugs",
   n.iter = 62000, n.burnin = 2000, n.thin = 100
)
post.list <- to.list(post.bugs)
post.mcmc <- to.mcmc(post.bugs)
save.image("output/result.RData")

計算時間はおよそ15秒でした。結果は以下の通り。wは収束はしたもののsdが大きいですね。pはいい感じです。

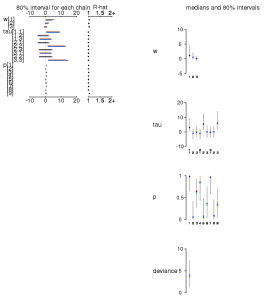
	mean	sd	2.5%	25%	50%	75%	97.5%	Rhat	n.eff
w[1]	1.98	2.42	-0.12	0.56	1.17	2.44	8.75	1.03	300
w[2]	0.81	1.11	-0.51	0.16	0.56	1.09	3.96	1.01	630
w[3]	0.12	1.05	-1.51	-0.36	0.03	0.47	2.57	1.03	1800
tau[1,1]	4.04	3.87	0.24	1.37	2.89	5.41	14.57	1.00	1800
tau[1,2]	-1.26	3.04	-8.11	-2.80	-1.01	0.38	4.36	1.00	1800
tau[1,3]	-0.13	3.10	-6.52	-1.78	-0.21	1.57	6.48	1.00	1800
tau[2,1]	-1.26	3.04	-8.11	-2.80	-1.01	0.38	4.36	1.00	1800
tau[2,2]	6.49	4.81	0.76	2.98	5.33	8.74	18.88	1.00	680
tau[2,3]	0.01	3.50	-7.34	-1.97	-0.05	1.98	7.13	1.00	1800
tau[3,1]	-0.13	3.10	-6.52	-1.78	-0.21	1.57	6.48	1.00	1800
tau[3,2]	0.01	3.50	-7.34	-1.97	-0.05	1.98	7.13	1.00	1800
tau[3,3]	7.04	5.15	0.82	3.18	5.80	9.51	20.48	1.00	980
p[1]	0.90	0.17	0.40	0.86	0.99	1.00	1.00	1.01	1600
p[2]	0.14	0.18	0.00	0.00	0.06	0.23	0.63	1.00	1400
p[3]	0.62	0.25	0.12	0.43	0.63	0.82	1.00	1.01	420
p[4]	0.78	0.23	0.24	0.63	0.86	0.99	1.00	1.00	1300
p[5]	0.16	0.20	0.00	0.00	0.06	0.26	0.70	1.00	740
p[6]	0.37	0.26	0.00	0.15	0.34	0.58	0.90	1.00	1300
p[7]	0.87	0.19	0.33	0.80	0.97	1.00	1.00	1.00	1500
p[8]	0.16	0.19	0.00	0.00	0.08	0.28	0.65	1.00	1300
p[9]	0.36	0.25	0.00	0.14	0.34	0.55	0.87	1.04	340
deviance	4.13	2.49	0.47	2.28	3.77	5.58	9.74	1.02	330

Testデータである最後の3人の購入する確率は以下のように算出されました（BUGSは分布のmedianを取りました）。

	infer.net	BUGS
Test1	0.96	0.97
Test2	0.16	0.08
Test3	0.29	0.34

さらに識別能力を上げるために2通りの方法があります。1つ目の方法は先ほどのBUGSコードにおいて、wの平均をゼロベクトルではなく、無情報な事前分布を導入することです。以下になります（変更部分だけ）。

w[1:N.w] ~ dmnorm(mn[], tau[,])
mn[1:N.w] ~ dmnorm(Zero[], Non.informative.tau[,])

実行するRコードも2行追加になります。

set.data("Non.informative.tau", diag(rep(1.0E-4, N.w), N.w))
set.param("mn", rep(0, N.w))

しかしながら今回はこれではデータ不足のため収束しませんでした。

2つ目の方法は線形カーネルではなくて他のカーネルを使うことです。MicrosoftのForumに2011/06/03に質問している方がいまして、詳しそうな方の返答によると以下になります。

minka replied on 05-04-2010 7:32 AM Infer.NET does not provide kernels, however you can simulate kernels using random feature expansion (Rahimi & Recht, "Random features for large-scale kernel machines", NIPS 2007). This technique replaces the kernel trick by mapping the data into a randomized feature space with finite dimension, such that the inner product of two randomly mapped data points is approximately the same as the value of a kernel function evaluated at the two data points. As a result, you obtain a random feature based classifier approximately equivalent to the kernelized classifier. Infer.NET does not automatically perform random feature expansion so you will have to write the code to generate these features, but the code should be quite simple.

とのことです。僕は機械学習のアルゴリズムには疎いのでこのあたりで一時退却としました。