infer.netの例題シリーズ5　Click model (改)

今回は「Short Examples: Click model」をやります。実はこの分析の強化版が「Longer Examples: Click through model」になっていまして、個人的には今回のデータだけでは教育用途かなと思いました。

とにかくデータと目的を紹介します。まずはデータですが以下のように3列からできています（合計522個）。

Judgement	Click	Exam
2	24	34
2	0	2
1	39	75
1	39	75
0	2	4
1	8	17
…	…	…
1	0	1
1	0	2

Exam: Googleの検索結果を思い浮かべて下さい。ページのサマリーが並んでいます。そのサマリーに「目を留めた」回数です。視線検知でデータをとったようです。
Click: 「目を留めた」中で実際にクリックにつながった回数です。
Judgement: クリック後のページが実際に「関係なし（0）」か「関係ありそう（1）」か「関係ある（2）」かを表しています。データの個数は0が93個, 1が363個, 2が66個です。

今回の目的はExamとClickからJudgementを予測することです。Infer.netの解説ページでは

The more examinations we have, the more we believe the evidence. We could think of the set of click/non-click events as the outcome of a binomial experiment - the probability of observing m clicks given N examinations is given by the binomial distribution Bin(m|N, m) where m is a parameter that we need to infer.

と書いてあり、2項分布のパラメータmを推測すればいいんじゃね？とのことですのでそれを実直に実装しました（ちなみにInfer.netのサンプルコードでは、教育目的のため上記とは異なったアプローチをとっています）。

BUGSコードは以下になりました。

model {
   for (i in 1:N){
      Click[i] ~ dbin(p[i], Exam[i])
      p[i] <- phi(x.p[i])
      x.p[i] ~ dnorm(mu.x.p[judge[i]], tau[judge[i]])

      Judge[i] ~ dcat(q[i,])
      judge[i] ~ dcat(q[i,])
      total.v[i] <- inprod(w[], v[i,])
      for (j in 1:N.judge) {
         q[i,j] <- v[i,j] * w[j] / total.v[i]
         v[i,j] <- exp(-pow(x.p[i] - mu.x.p[j], 2)*tau[j]*0.5) / sigma[j]
      }
   }
   for (j in 1:N.judge) {
      mu.x.p[j] ~ dnorm(0, 1.0E-4)
      log(w[j]) <- log.w[j]
      tau[j] <- 1/(sigma[j]*sigma[j])
      sigma[j] ~ dunif(0, 100)
   }
   log.w[1] ~ dnorm(0, 1.0E-4)
   log.w[2] ~ dnorm(0, 1.0E-4)
   log.w[3] <- 0
}

モデルを構築した際の基本の考え方は以下になります。

3行目：Click数はExam数とpの二項分布で決まる。
4～5行目：pはx.pのプロビット。x.pはjudgeごとに平均と分散が定められている正規分布から生成される。
7～13行目： x.pの値により、各judgeへの“近さ”（v）が決まり、その近さに重みをかけたものの割合（q）に応じてjudge（真の関連の程度）とJudge（実際の関連の程度）が決まる。
12行目： “近さ”（v）はx.pを生成した分布を流用し、正規分布で決める。変えてもいいと思います。
21～23行目：重みは無情報事前分布で与える。どれか一つは固定する。今回はデータが一番少ない「関係あり」の重み（log.w）を0としました。

キックするRコードは以下になりました。

source("R2WBwrapper.R")
d <- read.delim("input/data.txt", as.is=TRUE, sep="\t")
N <- nrow(d)
N.judge <- 3

clear.data.param()
set.data("N", N)
set.data("N.judge", N.judge)
set.data("Judge", d$Judgement+1)
set.data("Click", d$Click)
set.data("Exam", d$Exam)

set.param("x.p", rep(0, N))
set.param("mu.x.p", c(-2, 0, 2))
set.param("log.w", c(0, 0, NA))
set.param("sigma", rep(1, N.judge))

post.bugs <- call.bugs(
   n.chains = 3,
   file = "model/model.bugs",
   n.iter = 60000, n.burnin = 5000, n.thin = 50
)
post.list <- to.list(post.bugs)
post.mcmc <- to.mcmc(post.bugs)
save.image("output/result.RData")

2時間弱で収束しました。結果は以下になります。最初に各データにおける推定されたx.pの値のmedianはすべて[-2.5, 2.5]の範囲に収まっていました。そして以下の図は各judgeへの近さ（v）に重みをかけたものの分布になります。

f:id:StatModeling:20201114161723p:plain

以下の図は上記のものの割合（q）を表した分布になります。

f:id:StatModeling:20201114161718p:plain

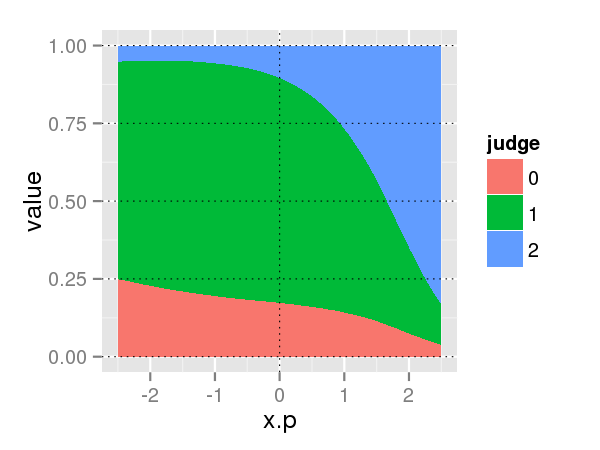
この図を見る限りは、pが低いところでは最頻値としてはjudge=1であり、pが0.8を超えたあたりからjudge=2になると解釈できます。

ここからさらにユーザ情報やページのサマリの位置（ランク）の情報によってモデルが複雑化していくようです。

StatModeling Memorandum

StanとRとPythonでベイズ統計モデリングします. たまに書評.

infer.netの例題シリーズ5　Click model (改)