少し前に週刊ダイヤモンドの記事「使える大学・使えない大学」の結果がインターネット上で話題になっていました。具体的には以下のデータです。

引用元はこちら(参考: Googleブックスの書籍を引用するには)
画像の下の方の注意書きにも注目。有効回答数は「使える大学」と「使えない大学」で異なっています。1位~5位を5点~1点にして集計した結果のようです。そして「使える度合い」の算出方法には「使える大学」の点数と「使えない大学」の点数の差を使っています。
点数の差で問題ナシと言う人もします。しかしながら、例えば大学Aが「使える点数10100, 使えない点数10000」で大学Bが「使える点数100, 使えない点数0」である時、それが等価に思えるでしょうか。少なくとも僕にはそうは思えませんでした。
また点数の割合がいいんじゃないかという人もいます。色々な割算値が提案されているようです。回答数ならまだしも点数の割合…うーん気持ち悪いです。例えばこの記事の方法では大学Aが「使える点数0, 使えない点数1」で大学Bが「使える点数0, 使えない点数100」の時に同じランクになります。やっぱ同じには思えませんね…。久保先生なら憤慨してKubolog行きになること間違いありません。
じゃあ僕ならどうするかをしばらく考えていました。現時点でのベストの処理方法の結論が出たので記事にします。
まず分かったのは集計後の点数では、情報がだいぶ落ちてしまっていて、大学ごとの「使える度合い」を推測するのはかなり厳しいということです。ですので、以降はいつか生データが入手できた時のための妄想になります。すみません。その生データがどんなものであればよいか?僕の想定は以下のようなアンケートです。
上位5名の中で大学がかぶることもあることに注意しましょう。本当はさらに職場の人数が分かるとよいのですが、今回は得られないとしましょう。あなたの職場で使える人、使えない人、それぞれ上位5名を思い浮かべて下さい。次にその人たちの出身大学を順に記入してください。
もし、以下のようなアンケートだとどうなるでしょうか。
これですと職場の話ではなくニュースや論文などのイメージが影響してしまう可能性があります。また、仮に職場にいる人を思い浮かべていたとしても、ある大学に所属する人が複数人いた場合、「使える」を聞く際にはその「使える度合い」が複数人のうちでmaxの人が、「使えない」を聞く際にはminの人が思い浮かべられることになりそうです。これも情報を失っていて、よいモデリングの妨げとなります。使える大学、使えない大学、それぞれ上位5校を記入してください。
前置きが長くなりましたが、今回の妄想アンケートのデータは以下になります(データを生成するRコードは記事の最後にあります)。
| worst1 | worst2 | worst3 | worst4 | worst5 | best5 | best4 | best3 | best2 | best1 |
|---|---|---|---|---|---|---|---|---|---|
| 16 | 30 | 7 | 2 | 19 | 4 | 15 | 4 | 2 | 29 |
| 7 | 5 | 7 | 7 | 6 | 13 | 25 | 11 | 6 | 7 |
| 12 | 12 | 23 | 3 | 23 | 6 | 7 | 8 | 9 | 11 |
| 1 | 2 | 22 | 2 | 8 | 24 | 4 | 7 | 7 | 5 |
| 3 | 15 | 26 | 6 | 30 | 4 | 26 | 22 | 13 | 11 |
| … | … | … | … | … | … | … | … | … | … |
| 8 | 6 | 6 | 5 | 8 | 4 | 7 | 22 | 24 | 11 |
| 1 | 12 | 2 | 7 | 7 | 6 | 4 | 4 | 5 | 9 |
| 30 | 30 | 30 | 30 | 26 | 2 | 2 | 15 | 4 | 11 |
| 3 | 3 | 26 | 4 | 7 | 9 | 7 | 15 | 11 | 11 |
| 7 | 6 | 6 | 3 | 2 | 24 | 22 | 26 | 24 | 4 |
1行ごとにアンケートの回答になっています。数字は大学のインデックスです。簡単のため、アンケート回答数(V)は50個、選択肢となるべき大学数(U)は30(インデックスは1~30)、職場の人数(W)はおおよそどこも同じで20と仮に定めました。最後のWは大きいと計算時間がかかるようになります。実際に僕が使う場合にはWを20, 40, 60, 80という振り方をしてWAICを比較することになりそうです。
こういうややこしいデータを相手にモデリングする際に重要なのは、はじめは最も簡単な場合を想定してモデリングすることです。今回ですと、1行だけのデータに対してモデリングすることを考えてみましょう。また、W=10、すなわち職場にいる人は10人で使える5名、使えない5名で全員と考えましょう。すると、以下のようなStanコードになりました。
data { int U; int Worst_and_Best[10]; vector<lower=0>[U] Alpha; } parameters { simplex[U] theta; ordered[10] performance; vector[U] mu_pf; real<lower=0> s_mu; } model { theta ~ dirichlet(Alpha); mu_pf ~ normal(0, s_mu); for(k in 1:10){ Worst_and_Best[k] ~ categorical(theta); performance[k] ~ normal(mu_pf[Worst_and_Best[k]], 1); } }
- 3行目: ここに大学のインデックスが入ります。順序は使える度合いが小さい順、すなわち使えない→使える順に並んでいるとします。
- 4,8,15行目: 大学によって人数が違いますし、職場への入りやすいさも違います。そこで、職場におけるある大学出身者の存在確率を
thetaで表し、事前分布としてディリクレ分布を使っています。また、職場ごとの業種の情報とかはないので、ここでは全職場で共通のthetaを使うことにします。 - 9行目:
performance[k]はk番目の人の使える度合いを表しています。これが順に並んでいることが制限ですので、Stanのordered vectorを使えばバッチリです。このモデルのキモです。 - 19~20行目: 大学のインデックスがカテゴリカル分布
thetaから決まり、インデックスに応じて平均が異なる正規分布(平均mu_pf[u], 標準偏差1の正規分布)からperformanceが生成されています。現実はもっと裾の長い分布のようなイメージがありますが、はじめは正規分布を使います。 - 16行目:
mu_pfにも縛りを入れて、平均0, 標準偏差s_muの正規分布から生成されると考えます。s_muは無情報事前分布にしています。
このモデリングのいいところは、最終的に大学ごとにmu_pfが得られるので、その大小を持って「使える大学」「使えない大学」を定量的に判断することができます。
次に、先ほどデータ1行だったのをV行まで考慮し、職場で順位が不明の人が(W-10)人いるとして拡張したものが以下のStanコードになります。
data { int V; # num of voter int U; # num of university int W; # num of worker int Worst[V,5]; int Best[V,5]; vector<lower=0>[U] Alpha; } parameters { simplex[U] theta; ordered[W] performance[V]; vector[U] mu_pf; real<lower=0> s_mu; } model { theta ~ dirichlet(Alpha); mu_pf ~ normal(0, s_mu); for (v in 1:V){ for (k in 1:5){ Worst[v,k] ~ categorical(theta); performance[v,k] ~ normal(mu_pf[Worst[v,k]], 1); } for (k in 6:(W-5)){ real gamma[U]; for (u in 1:U) gamma[u] <- log(theta[u]) + normal_log(performance[v,k], mu_pf[u], 1); increment_log_prob(log_sum_exp(gamma)); } for (k in 1:5){ Best[v,k] ~ categorical(theta); performance[v,W-5+k] ~ normal(mu_pf[Best[v,k]], 1); } } }
- 26~31行目: 順位が分からない人たちはどこの大学かも分かりません。そこでトピックモデルの時と同じように大学のインデックスに対してsumming outする必要があります(summing outについてはこの記事参照)。各
kごとにthetaが重みの混合正規分布から生成したと考えていることに相当します。このループはV*(W-10)*U回まわりますので時間がかかるようになります。
キックするRコードは以下になります。
library(rstan) rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores()) d <- read.delim("input/data.txt", sep="\t") V <- nrow(d) U <- 30 W <- 20 Worst <- d[ , 1:5] Best <- d[ , 6:10] Alpha <- rep(1, U) set.seed(123) data <- list( V = V, U = U, W = W, Worst = Worst, Best = Best, Alpha = Alpha ) stan_fit <- stan(file="model/model.stan", data=data, pars=c('theta', 'mu_pf', 's_mu'),iter=1000, warmup=200, thin=2)
計算時間はSurface Pro 3(core i5)でおよそ1chainあたり13分でした。バッチリ収束です。
以降、結果になります。一番重要なmu_pfは以下のようになりました。
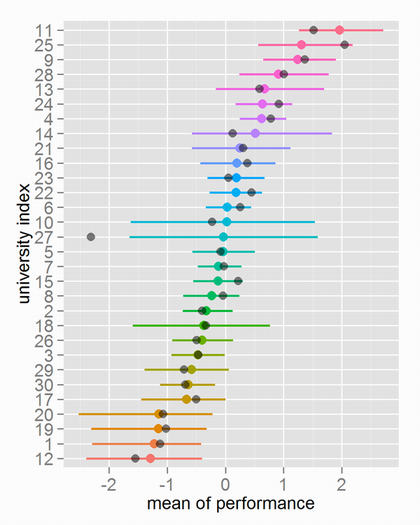
カラーの点は推定された大学ごとのmu_pfのMCMCサンプルの中央値、カラーの線は同じく95%信用区間です。黒い点は元データを生成する時に使った真の値になります。大学ごとの使える度合いはなかなかうまく表せていると思うのですがどうでしょうか。ちなみに大ハズレの大学インデックス27は、生成したデータに1つも入っていなかったのでこの結果は仕方ありません。
[おまけ] 職場におけるある大学出身者の存在確率であるthetaの結果は以下です。
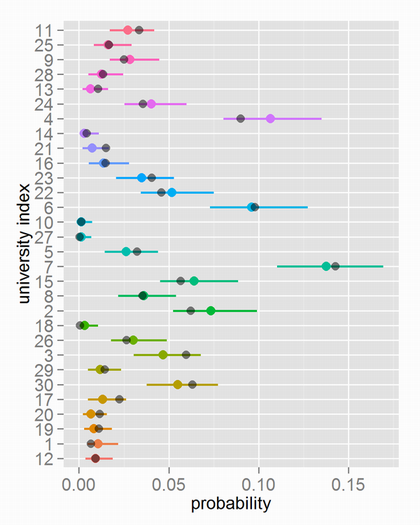
生データを見ると分かるのですが、さすがにランクでよく出ているところがthetaが高くなっていますね。
補足です。上記ではperformanceを生成するところの正規分布の標準偏差を、大学によらず1にしておきました。これは現時点でそこを拡張するとものすごく推定に時間がかかるようになってしまい、使いものにならないためです。データ数がもっと増えて、候補の大学数も増えて、変分ベイズがStanに実装されて速度の懸念がなくなった時には、そこが拡張できると思います。すると、大学ごとに使える人と使えない人を大きなバラツキで生成する大学…というものも分かるようになると思います。イメージでは東大よりも京大の方がバラツキが大きそうです。
その時のためにそのStanコードの一例を載せておきます。
data { int V; # num of voter int U; # num of university int W; # num of worker int Worst[V,5]; int Best[V,5]; vector<lower=0>[U] Alpha; } parameters { simplex[U] theta; ordered[W] performance[V]; vector[U] mu_pf; vector<lower=0>[U] s_pf; real<lower=0> s_mu; } model { theta ~ dirichlet(Alpha); mu_pf ~ normal(0, s_mu); s_pf ~ gamma(1, 1); for (v in 1:V){ for (k in 1:5){ Worst[v,k] ~ categorical(theta); performance[v,k] ~ normal(mu_pf[Worst[v,k]], s_pf[Worst[v,k]]); } for (k in 6:(W-5)){ real gamma[U]; for (u in 1:U) gamma[u] <- log(theta[u]) + normal_log(performance[v,k], mu_pf[u], s_pf[u]); increment_log_prob(log_sum_exp(gamma)); } for (k in 1:5){ Best[v,k] ~ categorical(theta); performance[v,W-5+k] ~ normal(mu_pf[Best[v,k]], s_pf[Best[v,k]]); } } }
- 14,26,31,36行目: 変更点です。
- 21行目: 勝敗データから強さを推定した時の過去の経験から
s_pfの事前分布は無情報事前分布では収束しなさそうです。何かしら設定する必要があると思います。
最後に今回の疑似アンケートデータを生成したRコードになります。自由に使ってください。
library(gtools) set.seed(123) V <- 50 # num of voter U <- 30 # num of university W <- 20 # num of workers per voter alpha.true <- rep(1, U) theta.v <- as.vector(rdirichlet(1, alpha.true)) mu.v <- rnorm(U, mean=0, sd=1) sigma.v <- exp(rnorm(U, mean=0, sd=0.1)) df <- t(sapply(1:V, function(v){ z <- sample(x=1:U, size=W, prob=theta.v, replace=T) pf <- sapply(z, function(x) rnorm(1, mean=mu.v[x], sd=sigma.v[x])) z.sorted <- z[order(pf)] z.sorted[c(1:5, (W-4):W)] })) colnames(df) <- c(paste('worst', 1:5, sep=''), paste('best', 5:1, sep='')) write.table(df, file='data.txt', sep="\t", quote=F, row.name=F, col.name=T)
追記
後日、この内容で東京Rで発表を行いました。スライドは以下です。