二つの時系列データの間に「差」があるか判断するには

詳しい経緯はこのまとめを参照してください。時間軸でぶった切って各時点で検定を使う手法は、百歩譲って「差があるかどうか」は判定できるかもしれないけど、「どれほど異なるのか」については何も言えない。「どの時刻から異なるか」についても言えるか分からない。そこでベイズ統計モデリングで判断しようと思います。ベイズ統計モデリングでは多くの事前知識を仮定としてモデルに組み込みますが、検定も多くの仮定を前提にしている点は同様と思います。

データは雰囲気だけ似せて自作しました。野生型100個体、変異体10個体で1～24まで1時間ずつ測定して24時点としました。まとめを見ると144時間みたいですが24時間に簡略化します。データの構成は以下です。

type	X1	X2	…	X23	X24
0	0.071	0.555	…	-0.236	-0.597
0	0.445	0.483	…	-0.149	0.231
0	0.225	0.764	…	-0.116	-0.213
…	…	…	…	…	…
1	0.28	0.379	…	-0.255	-0.289
1	0.756	0.432	…	-0.592	0.162
1	0.493	0.142	…	-0.437	-0.038

平均と±標準偏差のエラーバーつきで図にすると以下になります。

モデル1

はじめに考えたモデルは以下です。

各時刻で野生型と変異体と同じ状態空間モデルに従うベースラインを持つとする。変異体はそれに加えて定数の項（または指数関数で落ちる項）を付け加えて、変化点検出込みでモデリング。推定後、定数の高さのベイズ信頼区間から判定、でよさそう。 https://t.co/Aq0WDCC6P3

— .(@berobero11) 2016, 2月 16

モデル式にしますと以下になります。

元データは綺麗なsinカーブでしたが、ここでは一般の時系列でも通用する状態空間モデルを使っています。ここで、が野生型と変異体で共通のベースラインを表し、ランダムウォークで時間変化するとしています。野生型はこのベースラインに観測ノイズを加えて観測値になるとします。変異体はこのベースラインに特有の変化分が加わって、さらに観測ノイズを加えて観測値になるとします。この変化分は、どの時刻から入るか分からないし、どれくらいの大きさが加わるか分からないので、パラメータとしデータから推定します。どの時刻からがに相当し、どれくらいの間がに相当し、どれくらい大きさがに相当します。

状態空間モデルを使った推定については岩波データサイエンスvol.1, vol.6が充実しています。また、この変化点検出のモデルは、BUGS Book　11.7.1節を参考にしています。

岩波データサイエンス Vol.1

岩波データサイエンス Vol.6

The BUGS Book (Chapman & Hall/CRC Texts in Statistical Science)

Stanで実装すると以下になります。

data {
  int N_time;  # num of time points
  int N0;      # num of wild types
  int N1;      # num of variants
  int X[N_time];
  vector[N_time] Y0[N0];
  vector[N_time] Y1[N1];
}

parameters {
  vector[N_time] mu;
  real<lower=0> s_mu;
  real<lower=0> s_Y;
  real<lower=0, upper=1> diff;
  real<lower=1, upper=24> cp1;
  real<lower=0, upper=23> period;
}

transformed parameters {
  vector[N_time] y1_mean;
  for (t in 1:N_time)
    y1_mean[t] <- mu[t] + if_else(cp1 < t && t < cp1+period, diff, 0);
}

model {
  for (t in 2:N_time)
    mu[t] ~ normal(mu[t-1], s_mu);
  for (n in 1:N0)
    Y0[n] ~ normal(mu, s_Y);
  for (n in 1:N1)
    Y1[n] ~ normal(y1_mean, s_Y);
}

• 3～4行目：「0」がついている方が野生型、「1」がついている方が変異体です。
• 22行目：Stanではこのようにif_else文を使うことができます。
• 29行目：for (t in 1:N_time) Y0[n,t] ~ normal(mu[t], s_Y); と同じ意味です。Stanのvector型を使うとこのように短縮形で書くことができ、関数を呼ぶ回数が減るので実行速度が速くなります。
• 31行目：29行目と同様です。

推定結果は以下になります。diffの95%ベイズ信頼区間が0を含んでおらず、野生型と変異体の差はあると言えるでしょう。

	mean	se_mean	sd	2.5%	25%	50%	75%	97.5%	n_eff	Rhat
mu[1]	0.23	0.00	0.03	0.17	0.21	0.23	0.25	0.29	887	1.01
mu[2]	0.49	0.00	0.03	0.44	0.48	0.49	0.51	0.55	843	1.01
…	…	…	…	…	…	…	…	…	…	…
mu[23]	-0.27	0.00	0.03	-0.33	-0.29	-0.27	-0.25	-0.22	1107	1.00
mu[24]	0.04	0.00	0.03	-0.02	0.02	0.04	0.06	0.10	1151	1.00
s_mu	0.20	0.00	0.03	0.15	0.18	0.20	0.22	0.28	401	1.00
s_Y	0.31	0.00	0.00	0.30	0.31	0.31	0.31	0.32	1254	1.00
diff	0.32	0.00	0.05	0.23	0.29	0.32	0.36	0.42	174	1.01
cp1	6.45	0.01	0.35	5.56	6.21	6.47	6.73	6.97	568	1.00
period	5.69	0.04	0.74	4.30	5.16	5.71	6.20	7.15	323	1.01
y1_mean[1]	0.23	0.00	0.03	0.17	0.21	0.23	0.25	0.29	887	1.01
…	…	…	…	…	…	…	…	…	…	…
y1_mean[24]	0.04	0.00	0.03	-0.02	0.02	0.04	0.06	0.10	1151	1.00
lp__	1798.55	0.13	3.78	1790.09	1796.25	1798.90	1801.24	1804.94	797	1.00

共通のベースライン（mu；左図）と、変異体と野生型の差（右図）を描画すると以下になります。

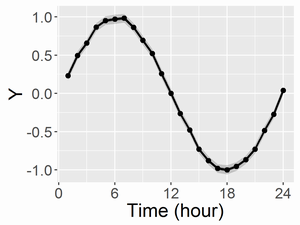
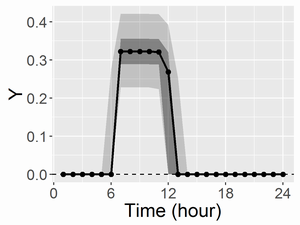
ここで、黒点とつなぐ線はMCMCサンプルの中央値、濃い灰帯は50%ベイズ信頼区間、薄い灰帯は95%ベイズ信頼区間です。

このモデルでは差を「一定期間の定数」と仮定していますが、定数じゃないかもしれません。また、変化点の外側でも差がある可能性を残す方が自然に思えます。そして、このようなif文を使ったMCMCが非効率的で初期値の設定もシビアな上に計算に時間を要します（1chainあたり5分ぐらいですが）。そこで、モデル2を考えました。

モデル2

モデル式は以下です。

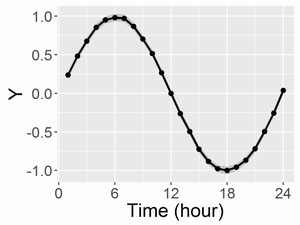
システムモデルの変化がなめらかであるとして、2階差分に変更しました（ちなみにモデル1で2階差分に変更すると、さらに推定に時間がかかります）。そして、野生型と変異体の差の部分も時間変化するようにし、スイッチ的な変動が予想されるので、変化点検出を考慮してシステムモデルにコーシー分布を使いました（この記事参照）。

data {
  int N_time;
  int N0;
  int N1;
  int X[N_time];
  vector[N_time] Y0[N0];
  vector[N_time] Y1[N1];
}

parameters {
  vector[N_time] mu;
  real di0;
  vector<lower=-pi()/2, upper=pi()/2>[N_time-1] di_unif;
  real<lower=0> s_mu;
  real<lower=0> s_di;
  real<lower=0> s_Y;
}

transformed parameters {
  vector[N_time] di;
  vector[N_time] y1_mean;
  di[1] <- di0;
  for (t in 2:N_time)
    di[t] <- di[t-1] + s_di*tan(di_unif[t-1]);
  y1_mean <- mu + di;
}

model {
  for (t in 3:N_time)
    mu[t] ~ normal(2*mu[t-1] - mu[t-2], s_mu);
  for (n in 1:N0)
    Y0[n] ~ normal(mu, s_Y);
  for (n in 1:N1)
    Y1[n] ~ normal(y1_mean, s_Y);
}

• 13,15,24行目など：コーシー分布を使った状態変化はそのまま実装すると収束しません。一様分布に従うパラメータから変数変換で作るのがポイントです。
• 25行目：for (t in 1:N_time) y1_mean[t] <- mu[t] + mu[di];をvector型の活用によって短縮しています。
• 30行目：2階差分にしています。

こちらは計算時間は1chainあたり約15秒でした。推定結果は以下の通り。 共通のベースライン（mu；左図）と、変異体と野生型の差（di；右図）を描画すると以下になります。凡例は先ほどの図と同じです。

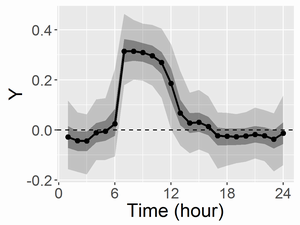
diの95%ベイズ信頼区間が0を含んでいない期間が差がある期間と言えるでしょう。さらに、どこから差がありそうなのか、どれほど差がありそうなのかも確率付きで述べることができます。

最後に、参考までに実行するRコードは以下になります。

library(rstan)
# rstan_options(auto_write=TRUE)
# options(mc.cores=parallel::detectCores())

# prepare data
d <- read.csv('input/data.txt')
N_time <- 24
X <- 1:24
d0 <- subset(d, type==0)
d1 <- subset(d, type==1)
data <- list(N_time=N_time, N0=nrow(d0), N1=nrow(d1), X=X, Y0=d0[,-1], Y1=d1[,-1])

# model1
stanmodel1 <- stan_model(file='model/model1.stan')
fit1 <- sampling(stanmodel1, data=data,
  init=function() { list(mu=colMeans(d0[,-1]), diff=0.2, cp1=7, period=6) },
  iter=4500, warmup=500, seed=123
)

# model2
stanmodel2 <- stan_model(file='model/model2.stan')
fit2 <- sampling(stanmodel2, data=data,
  init=function() { list(mu=colMeans(d0[,-1])) },
  iter=1500, warmup=500, seed=123
)

• 16行目：シビアな初期値設定に注目してほしいです。
• 17行目：モデル1ではMCMCの自己相関が強く、iterを4500にしています。

データを作成したRコードは以下になります。

set.seed(1)

N_time <- 24
N0 <- 100
N1 <- 10
Add_y <- 0.3
Add_x <- 7:12
SD <- 0.3

x <- 1:N_time
y0 <- sin(x/N_time*2*pi)
y1 <- y0
y1[Add_x] <- y1[Add_x] + Add_y

Y0 <- round(matrix(rnorm(N_time*N0, y0, SD), nrow=N0, byrow=TRUE), digits=3)
Y1 <- round(matrix(rnorm(N_time*N1, y1, SD), nrow=N1, byrow=TRUE), digits=3)
d <- rbind(data.frame(type=0, Y0), data.frame(type=1, Y1))
write.table(d, file='input/data.txt', row.names=F, sep=',', quote=F)