陽に解ける常微分方程式を使ったモデル

今回はデータの背後に簡単な（陽に解ける）常微分方程式で記述できるダイナミクスがあると仮定して、Stanでパラメータの推定を行いたいと思います。

状況として定期的に（例えば一年ごとに）サービスをリリースした場合を考えます。それらのサービスを使う総利用者数の時系列があるとします。そして各サービスともリリース直後は盛り上がってくるものの、じわじわと利用者が減っていくとします。今回はその利用者がどのサービス由来かわからないとして解析します（どのサービス由来か分かればもっと簡単にできます）。また今回のデータ取得期間はt=1:100でt=0,40,80に計3つの新規サービスをリリースしたと分かっているとし、グラフは以下のようになっているとします（縦軸の単位は[百人]とか）。

さてこの時系列を解析するうえで「リリース直後は盛り上がってくるものの、じわじわ減る」というダイナミクスをモデルに反映するのが大切となります。これをなるべくシンプルな常微分方程式で記述したいとすると、以下のような単純な流入項と流出項のある常微分方程式が考えられます。Xはまだサービスを使っていないが結果的に使うことになる利用者数、Yはある時刻における利用者数です。は流入速度係数, は流出速度係数です。

これは陽に解けて、特に変数Yは以下の式になります。

はある時刻の利用者数の上限に関係する定数です。例えばパラメータがの時の変数Yの挙動は以下のような時系列になります。

この3パラメータ（）の式を使ってStanでフィッティングしていきます。Stanコードは以下にな りました。

data {
   int<lower=1> N_times;
   real<lower=0> Y[N_times];
}
parameters {
   vector<lower=0, upper=1.0>[3] k_up;
   real<lower=0, upper=min(k_up)> k_down;
   vector<lower=0, upper=10>[3] a_const;
   real<lower=0, upper=10> alpha;
   real<lower=0> s_noise;
}
transformed parameters {
   vector<lower=0>[N_times] y_service[3];
   vector<lower=0>[N_times] y_hidden;
   for (t in 1:N_times){
      y_service[1,t] <- a_const[1]*(exp(-k_down*t) - exp(-k_up[1]*t));
      y_service[2,t] <- if_else(t > 40, a_const[2]*(exp(-k_down*(t-40)) - exp(-k_up[2]*(t-40))), 0.0);
      y_service[3,t] <- if_else(t > 80, a_const[3]*(exp(-k_down*(t-80)) - exp(-k_up[3]*(t-80))), 0.0);
      y_hidden[t] <- alpha + y_service[1,t] + y_service[2,t] + y_service[3,t];
   }
}
model {
   Y ~ normal(y_hidden, s_noise);
}

• 6～8行目: 今回はk_up, a_const はサービスごとに異なるとし、k_down は各サービスで共通としました。
• 7行目: k_up > k_down でないと「リリース直後は盛り上がってくるものの、じわじわ減る」という時系列にはなりませんのでその条件になります。
• 16～18行目: 陽に解いた式をそのまま使用しています。過去のサービスの利用者も積み重なっていくのでこのようになります。

キックするRコードは省略します。データを渡す時に100で割って適度にスケーリングして渡しました。

結果は以下になりました。

	mean	se_mean	sd	X2.5.	X25.	X50.	X75.	X97.5.	n_eff	Rhat
k_up[1]	0.49	0.01	0.12	0.29	0.41	0.48	0.57	0.78	395	1.01
k_up[2]	0.14	0.00	0.02	0.10	0.13	0.14	0.15	0.18	627	1.00
k_up[3]	0.28	0.00	0.06	0.19	0.24	0.27	0.31	0.42	1009	1.00
k_down	0.0064	0.0001	0.0022	0.0030	0.0049	0.0062	0.0076	0.0119	391	1.00
a_const[1]	1.20	0.01	0.23	0.81	1.03	1.18	1.34	1.71	438	1.01
a_const[2]	1.13	0.01	0.14	0.90	1.04	1.11	1.20	1.46	480	1.00
a_const[3]	0.82	0.00	0.10	0.65	0.75	0.81	0.88	1.05	542	1.00
alpha	0.78	0.01	0.24	0.24	0.64	0.81	0.95	1.19	384	1.01
s_noise	0.094	0.000	0.007	0.081	0.089	0.093	0.098	0.108	1356	1.00

この記事の最後にデータを生成したRコードを載せていますが、真の値をかなりよく推定できています。

データ上の利用者数（黒の○点）、ノイズ項を除いた真の利用者数（黒の点線）、その推定されたMCMCサンプルの中央値（青の実線）、同95%信用区間（グレーの帯）をプロットしたものが以下になります。

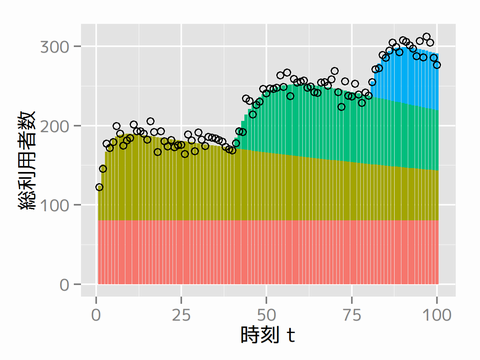
また切片＋3つのサービスの利用者数に分けて推定された値（MCMCサンプルの中央値）を積み重ね棒グラフでプロットしたものが以下になります。

ちなみにダイナミクスが複雑で常微分方程式が陽に解けない場合は、パラメータをMCMCで探索しながら微分方程式を解くといったことを繰り返す必要があり、StanではODEの機能として実装されています（Stanのマニュアルの「19. Solving Differential Equations」の章）。

最後にこの記事のデータを生成するRコードは以下でした。

N.times <- 100
times <- 1:N.times
k.up1 <- 0.34
k.up2 <- 0.12
k.up3 <- 0.25
k.down <- 0.008
A1 <- 1.0
A2 <- 1.2
A3 <- 0.8
s.true <- 0.1
set.seed(123)

y1.true <- A1*(exp(-k.down*times) - exp(-k.up1*times))
y2 <- A2*(exp(-k.down*times) - exp(-k.up2*times))
y3 <- A3*(exp(-k.down*times) - exp(-k.up3*times))
y2.true <- c(rep(0,40), y2[1:(N.times-40)])
y3.true <- c(rep(0,80), y3[1:(N.times-80)])

y.true <- 1.0 + y1.true + y2.true + y3.true
y <- 100 * (y.true + rnorm(N.times, 0, s.true))
save.image("explicit_ode.RData")