トピックモデルシリーズ 3 UM （Unigram Mixtures）

次にUMを説明します。この記事の表記法は以下になります。

f:id:StatModeling:20201114135723p:plain

右2列は定数については数値を、そうでないものについてはR内の変数名を書いています。データは前の記事参照。グラフィカルモデルは以下になります（左: UM, 右: 前回のNB）。

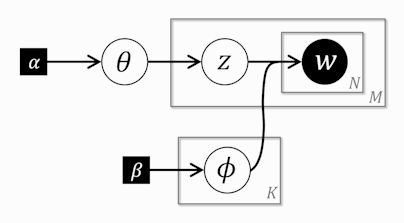
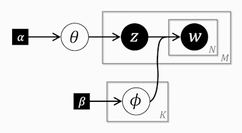
見比べてもらうと分かるのですが違う場所は文書ごとのトピックzがデータからパラメータ（潜在変数）になったところだけです。トピック情報を人手でつけるのは大変ですのでモデルの拡張としては非常に自然です。実はBUGSならば前回のNBのモデルのコードがそのまま使えます。Stanでは離散的なパラメータを簡単に扱うことがまだできなくて、現状ではその変数のとる値をすべて考慮して足しこむことで消去します（「marginalize out / marginalizing out」とか「sum out / summing out」とか呼ばれています）。この方法は単にそのままではできないからやるという否定的な意味合いだけではなくて、対数尤度の算出の高速化、ひいてはパラメータ推定の高速化に役立ちます。いつかはStanの内側で自動的によろしくやってくれる日が来ると思います。

summing outの方法ですが以下の図のように考えます。

f:id:StatModeling:20201114135730p:plain

まず文書ごとに独立と考えられるので、ある1つの文書mだけを考えます。そして、その『文書m内の』すべての単語の出現確率は、トピック1の目が出たとしてトピック1のサイコロ f:id:StatModeling:20201114134534p:plain からすべての単語が作られた確率＋トピック2の目が出たとしてトピック2のサイコロからすべての単語が作られた確率＋...＋トピックKの目が出たとしてトピックKのサイコロからすべての単語が作られた確率の和になります。これを数式で書くと以下になります。

f:id:StatModeling:20201114134515p:plain

このlogをとったものが『文書mの』log probabilityの増加分になります。ここで先にStanの関数であるlog_sum_exp()の練習をしておきます。log_sum_exp()は和の状態になっているものに対してlogを取りたいときに使います。以下のような変形になります。

f:id:StatModeling:20201114134519p:plain

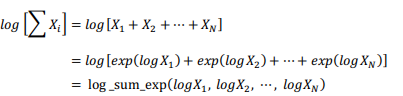
この変形のメリットは数値計算上の安定さのようです。最後のlog_sum_exp()の中身をarrayに格納しておくと、そのarrayごと引数に取ることもできます。それではlog_sum_exp()を使って、さきほどの『文書mの』log probabilityの増加分を求めてみます。以下のようになります。

f:id:StatModeling:20201114134546p:plain

最後に文書mのmを1～M回まで繰り返せばOKです。最終的に前回のStanコードの「likelihood」の部分は以下のように変わります。

data {
   int<lower=1> K;                    # num topics
   int<lower=1> M;                    # num docs
   int<lower=1> V;                    # num words
   int<lower=1> N;                    # total word instances
   int<lower=1,upper=V> W[N];         # word n
   int<lower=1,upper=N> Offset[M,2];  # range of word index per doc
   # hyperparameter
   vector<lower=0>[K] Alpha;     # topic prior
   vector<lower=0>[V] Beta;      # word prior
}
parameters {
   simplex[K] theta;      # topic prevalence
   simplex[V] phi[K];     # word dist for topic k
}
model {
   # prior
   theta ~ dirichlet(Alpha);
   for (k in 1:K)
      phi[k] ~ dirichlet(Beta);

   # likelihood
   for (m in 1:M){
      real gamma[K];
      for (k in 1:K){
         gamma[k] <- log(theta[k]);
         for (n in Offset[m,1]:Offset[m,2])
            gamma[k] <- gamma[k] + log(phi[k,W[n]]);
      }
      increment_log_prob(log_sum_exp(gamma));
   }
}

24行目：gammaはlog_sum_exp()の引数になる配列（array型）です。
26行目：theta[k]はのことです。log(.)の代わりにcategorical_log(k,theta)でもOKです。
28行目：phi[k,W[n]]はのことです。log(.)の代わりにcategorical_log(W[n],phi[k])でもOKです。
30行目：log probabilityの増加分はincrement_log_prob()を使ってStanに教えてあげます。結局StanではNBの時と同様、データからK面サイコロtheta（1個）、V面サイコロphi（K個）の形を推定することになります。

これをキックするRのコードは以下になります。

library(rstan)

load("input/201402_data1.RData")

data <- list(
   K=K,
   M=M,
   V=V,
   N=N.1,
   W=w.1$Word,
   Offset=offset.1,
   Alpha=rep(1, K),
   Beta=rep(0.5, V)
)

fit <- stan(
   file='model/UM.stan',
   data=data,
   iter=1000,
   thin=1,
   chains=1
)

前回のNBの時と比べると、文書のトピックをデータで渡さなくなった点が異なるだけです。21行目のchains=1となっている理由はStanのマニュアルの「15.2. The Difficulty of Bayesian Inference for Clustering」に書いてある通りです。具体的にはトピックのインデックスの順序はどうだっていいため、chainが異なると収束するインデックスがバラバラになる問題が発生します。そうすると通常のRhatは求めることができません。しかしStanはchain数が1つでもHMCサンプルの自己相関からRhatを求めてくれますので、それを確認することにします（もちろんtraceplotは見ます）。実際の解析では、初期値を振って1chainずつ流して最終的に知りたいこと（予測とか）が収束しているかをcheckすることになりそうです。

結果は以下になりました。文書あたりの単語数が少ないデータ（data1）ではパラメータが収束しませんでした。文書あたりの単語数が多いデータ（data2）では収束しましたが明らかにうまくいっていません。モデルがデータとあっていないと考えられます。次回に期待です。Stanはモデルが悪くても収束することがあるので注意です。参考までにdata2の時の推定されたthetaとphiは以下の通りです。

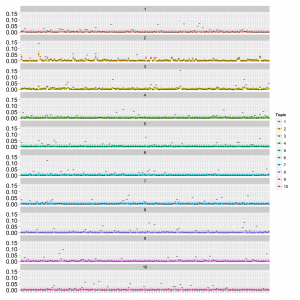
点はMCMCサンプルの中央値で範囲は80%信頼区間です。横軸はthetaではトピックのインデックス、phiでは単語のインデックスです。縦軸は確率です。真の値を黒の横棒で表しています。LDAを模したデータを作り方をしたのでUMのthetaは真の値と直接比較はできません。

最後にモデルのパラメータ数（Stanで出力される数です。ホントはsimplexの制限があるので実質的な数は少し減ります）や推定にかかった計算時間などは以下の通りです。

項目	文書あたりの単語数	NB	UM	LDA	LDA(Freq)	PAM	GaP
パラメータ数	少/多	1450	1450	？	？	？	？
計算時間	少	5.5m	2.3m	？	？	？	？
収束具合	少	○	×	？	？	？	？
lp__	少	-13892	-13882	？	？	？	？
計算時間	多	30.8m	11.7m	？	？	？	？
収束具合	多	○	○	？	？	？	？
lp__	多	-74154	-75760	？	？	？	？

StatModeling Memorandum

StanとRとPythonでベイズ統計モデリングします. たまに書評.

トピックモデルシリーズ 3 UM （Unigram Mixtures）