LDAの不満点の一つとしましては、トピック間の関係性を全て無視しているところです。例えば、「政治」と「経済」なんかは相関ありそうですよね。そういうトピック間の相関を考慮したモデルとしてはCTM(Correlated Topic Model)があります。実はStanのマニュアルでもCTMは実装されています(githubではここ)が、サンプルデータとサンプルプログラムをそのまま実行しても全く収束する気配がなくて殺意がわきます。またCTMの弱点としては2つのトピックの間の関係しか考慮されていないこと、また推定する分散共分散行列のパラメータ数がトピック数の2乗に比例して大きくなっていくという点が挙げられます。
そこで今回のPAM([Li+ 2006])を少し砕いて紹介して実装したいと思います。まずはこの記事の表記法は以下になります。前回の途中から使った単語の出現数(Frequency)を今回も使います。

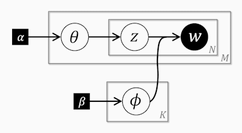
右2列は定数については数値を、そうでないものについてはR内の変数名を書いています。データは前の記事参照。 今回実装したグラフィカルモデルは以下になります(左: PAM, 右(参考): 前回のLDA)。
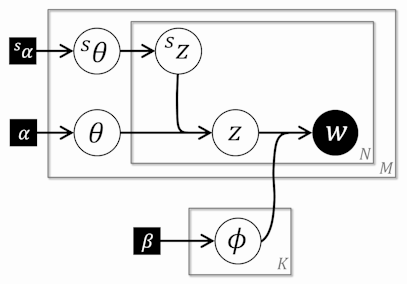
LDAと異なる点はトピックの階層を設定した点です。例えば、「再生医療」「バイオベンチャー」「金融危機」といったトピックがあるとします。その上位トピック(スーパートピックと呼びます)には「医療」「経済」といったものが考えられます。「バイオベンチャー」なんかは両方のスーパートピックから出やすそうなトピックですよね。以下の吹き出しの順に説明していきます。

①
ここではハイパーパラメータ からディリクレ分布に従って『文書の数だけ』
からディリクレ分布に従って『文書の数だけ』 が生成されます。この
が生成されます。この は『文書内の単語ごとの』スーパートピックを決める、いびつなS面サイコロです。文書ごとに形が変わります。この記事内では
は『文書内の単語ごとの』スーパートピックを決める、いびつなS面サイコロです。文書ごとに形が変わります。この記事内では を「スーパートピック分布」または「スーパートピック混合比」と呼びます。
を「スーパートピック分布」または「スーパートピック混合比」と呼びます。
②
ある文書内の『単語ごとに』にスーパートピックを決めます。文書が変わるとスーパートピックを決めるサイコロが変わります。
③
ここではハイパーパラメータ に従って『文書の数×スーパートピック数の数だけ』
に従って『文書の数×スーパートピック数の数だけ』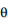 が生成されます。この
が生成されます。この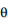 はLDAの時と同様の『文書内の単語ごとの』トピックを決める、いびつなK面サイコロです。
はLDAの時と同様の『文書内の単語ごとの』トピックを決める、いびつなK面サイコロです。
④
ある文書内の『単語ごとに』にトピックを決めます。文書もしくはスーパートピックが変わるとトピックを決めるサイコロが変わります。
残りはNB,UM,LDAと同じです。まとめますと以下の図のようになります。

PAMは本来DAG構造ならなんでも表現できますが、一番シンプルなバージョンアップということで、単純に1つだけ階層を深くした上記のグラフィカルモデル(four level PAM)がよく使われるようです。統数研の講座によりますと単純に階層を深くしていくのも有効な戦略とのことでした。
次にStanでの実装にうつります。まずはイメージしやすいようにStanがいつか離散パラメータを許してくれた時のStanコードを示します。
data { int<lower=1> K; # num topics int<lower=1> S; # num super topics int<lower=1> M; # num docs int<lower=1> V; # num words int<lower=1> N; # total word instances int<lower=1,upper=V> W[N]; # word n int<lower=1> Freq[N]; # frequency of word n int<lower=1,upper=N> Offset[M,2]; # range of word index per doc vector<lower=0>[S] Alpha_S; # super topic prior vector<lower=0>[K] Alpha[S]; # topic prior vector<lower=0>[V] Beta; # word prior } parameters { simplex[S] theta_S[M]; # super topic dist for doc m simplex[K] theta[M,S]; # topic dist for (doc m, super topic s) simplex[V] phi[K]; # word dist for topic k int<lower=1,upper=S> z_S[N]; # FUTURE: super topic index for word n int<lower=1,upper=K> z[N]; # FUTURE: topic index for word n } model { # prior for (m in 1:M){ theta_S[m] ~ dirichlet(Alpha_S); for (s in 1:S) theta[m,s] ~ dirichlet(Alpha[s]); } for (k in 1:K) phi[k] ~ dirichlet(Beta); # likelihood for (m in 1:M) { for (n in Offset[m,1]:Offset[m,2]) { z_S[n] ~ categorical(theta_S[m]); z[n] ~ categorical(theta[m,z_S[n]]); W[n] ~ categorical(phi[z[n]]); } } }
しかしながら、18-19行目が現状ではNGです。これらは離散パラメータなのでsumming outしなくてはなりません。今までと同様、文書ごとに独立と考えられるので、ある1つの文書mだけを考えて『文書mの』log probabilityの増加分を考えますと以下になります。

log_sum_exp()が入れ子になっています。まぁ慣れですね。最後に文書mのmを1~M回まで繰り返せばOKです。実際のStanの実装は以下のようになります。
data { int<lower=1> K; # num topics int<lower=1> S; # num super topics int<lower=1> M; # num docs int<lower=1> V; # num words int<lower=1> N; # total word instances int<lower=1,upper=V> W[N]; # word n int<lower=1> Freq[N]; # frequency for word n int<lower=1,upper=N> Offset[M,2]; # range of word index per doc vector<lower=0>[S] Alpha_S; # super topic prior vector<lower=0>[K] Alpha[S]; # topic prior vector<lower=0>[V] Beta; # word prior } parameters { simplex[S] theta_S[M]; # super topic dist for doc m simplex[K] theta[M,S]; # topic dist for (doc m, super topic s) simplex[V] phi[K]; # word dist for topic k } model { # prior for (m in 1:M){ theta_S[m] ~ dirichlet(Alpha_S); for (s in 1:S) theta[m,s] ~ dirichlet(Alpha[s]); } for (k in 1:K) phi[k] ~ dirichlet(Beta); # likelihood for (m in 1:M) { for (n in Offset[m,1]:Offset[m,2]) { real gamma_S[S]; for (s in 1:S){ real gamma[K]; for (k in 1:K) gamma[k] <- log(theta[m,s,k]) + log(phi[k,W[n]]); gamma_S[s] <- log(theta_S[m,s]) + log_sum_exp(gamma); } increment_log_prob(Freq[n] * log_sum_exp(gamma_S)); } } }
結局StanではデータからS面サイコロtheta_S(M個)、K面サイコロtheta(M×S個)、V面サイコロphi(K個)の形を推定することになります。
これをキックするRのコードは以下になります。
library(rstan) load("input/201402_data1.RData") S <- 3 data <- list( K=K, S=S, M=M, V=V, N=N.2, W=w.2$Word, Freq=w.2$Freq, Offset=offset.2, Alpha_S=rep(1, S), Alpha=matrix(rep(1, S*K), S, K), Beta=rep(0.5, V) ) fit <- stan( file='model/PAM.stan', data=data, iter=1000, chains=1, thin=1 )
結果は以下になりました。
LDAの時と同様、1文書あたりの総単語数が少ない場合(data1; 20単語程度)は収束しましたがトピックが分離できていませんでした。1文書あたりの総単語数が多い場合(data2; 150単語程度)はぎりぎり収束しませんでした。しかしphiを見てみますと、かなりよく推定できていることが分かりました。

点はMCMCサンプルの中央値で範囲は80%信頼区間です。横軸:単語のインデックス、縦軸:確率でトピックごとにプロットしています。真の値を黒の横棒で表しています。PAMでやるにはトピック数が少ないかもしれません。もしくは文書あたりのデータがまだ足りないかもしれません。
最後にモデルのパラメータ数(Stanで出力される数です。ホントはsimplexの制限があるので実質的な数は少し減ります)や推定にかかった計算時間などは以下の通りです。
| 項目 | 文書あたりの単語数 | NB | UM | LDA | LDA(Freq) | PAM | GaP |
|---|---|---|---|---|---|---|---|
| パラメータ数 | 少/多 | 1450 | 1450 | 2440 | 2440 | 4740 | ? |
| 計算時間 | 少 | 5.5m | 2.3m | 7.7m | 7.4m | 16.6m | ? |
| 収束具合 | 少 | ○ | × | ○ | ○ | ○ | ? |
| lp__ | 少 | -13892 | -13882 | -16920 | -16919 | -23091 | ? |
| 計算時間 | 多 | 30.8m | 11.7m | 53.7m | 30.4m | 69.9m | ? |
| 収束具合 | 多 | ○ | ○ | ○ | ○ | △ | ? |
| lp__ | 多 | -74154 | -75760 | -76793 | -76787 | -83274 | ? |