トピックモデルシリーズ 7 DTM （Dynamic Topic Model） の一種

最後はおまけでLDAに時系列を組み合わせた実装を試してみたので紹介します。

今まで「文書」と呼んできたものを「ユーザー」、「単語」と呼んできたものを「アクセスしたWebページ（≒アクション）」と考えます。ユーザーが1日目～31日目までV種類のWebページにアクセスしたデータがあるとします。そしてユーザーの興味のあるトピックの分布（トピック混合比）が時間によって変化すると考えます。ある人は興味が移りやすく、またある人は移りにくいでしょう。そんな状況をモデリングします。

この記事の表記は以下です。1人あたり1時刻あたり150アクションぐらいというデータです（記事の最後にデータを生成したRコードを載せてあります）。

グラフィカルモデルは以下になります。

トピックごとの単語分布に比べて個々人のトピック混合比の方が移り変わるスピードが速いと考えられますので、今回は単語分布はどのタイムポイントでも同じを使うことにしました。一番の悩みどころはsimplexである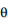の時間発展をどのようにモデリングするかです。色々試した結果では以下の方法がよさそうでした。変化の大きさを表すと 変化の方向を表すf:id:StatModeling:20201114134219p:plainを混ぜ合わせてとしました。一般的にMCMCサンプリングを用いる統計モデリングでは、このように「大きさ（scale）」と「方向」のような独立なパラメータに分離することで収束がよくなります。ちなみに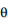のハイパーパラメータであるを時間発展させるモデルも考えられますが、各時点のから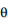が1つずつしか生成されないのでの推定がうまくいきません（収束しない）。NTTの岩田先生のモデルはが時間発展するものがいくつかあり、どうやって推定できているか一時期わかりませんでしたが、不動点反復法で求めていることを教えてもらいました。Gibbs samplingでは難しいと思います。

Stanの実装は以下になります。

data {
   int<lower=1> T;                      # num times
   int<lower=1> K;                      # num topics
   int<lower=1> M;                      # num users
   int<lower=1> V;                      # num actions
   int<lower=1> N;                      # total action instances
   int<lower=1,upper=V> W[N];           # action n
   int<lower=1,upper=N> Offset[T,M,2];  # range of action index per user
   int<lower=1> Freq[N];                # frequency of action n
   vector<lower=0>[K] Alpha0;           # pi prior
   vector<lower=0>[V] Beta;             # action prior
}

parameters {
   vector<lower=0,upper=1>[M] lambda;   # topic dist mobility of user m
   simplex[K] theta0[M];                # initial topic dist for user m
   simplex[K] pi[T-1,M];                # change direction of topic dist for (time t, user m)
   simplex[V] phi[K];                   # action dist for topic k
}

transformed parameters {
   simplex[K] theta[T,M];               # topic dist for (time t, user m)
   for (m in 1:M)
      theta[1,m] <- theta0[m];
   for (t in 2:T)
      for (m in 1:M)
         theta[t,m] <- (1-lambda[m])*theta[t-1,m] + lambda[m]*pi[t-1,m];
}

model {
   for(t in 2:T)
      for(m in 1:M)
         pi[t-1,m] ~ dirichlet(Alpha0);
   for (k in 1:K)
      phi[k] ~ dirichlet(Beta);

   for (t in 1:T) {
      for (m in 1:M) {
         for (n in Offset[t,m,1]:Offset[t,m,2]) {
            real gamma[K];
            for (k in 1:K)
               gamma[k] <- log(theta[t,m,k]) + log(phi[k,W[n]]);
            increment_log_prob(Freq[n] * log_sum_exp(gamma));
         }
      }
   }
}

• 15行目、今回は個々人の興味の移りやすさを表すlambdaは時刻によらないとして[0,1]の範囲の一様分布から推定します（Stanでは事前分布を設定しないと指定範囲の一様分布になる）。時刻が増えればlambdaは時刻に依存してベータ分布からstochasticに生成させてもよいかもしれません。ここは問題の背景によって色々変えることができます。例えば、普段はほとんど変化がなくてまれに大きく変化するような時系列をモデリングする場合には、lambdaは時刻に依存するとして、引数がともに1より小さいU字型のベータ分布から生成するようにします。
• 31～33行目は変化の方向をディリクレ分布から生成しています。

これをキックするRのコードは以下になります。今までどおりです。

library(rstan)

load("input/201402_data.DTM.RData")

data <- list(
   T=T,
   K=K,
   M=M,
   V=V,
   N=N.2,
   W=w.2$Word,
   Offset=offset.2,
   Freq=w.2$Freq,
   Alpha0=rep(1, K),
   Beta=rep(0.5, V)
)

fit <- stan(
   file='model/DTM.stan',
   data=data,
   pars=c('theta', 'phi', 'lambda'),
   iter=1000,
   chains=1,
   thin=1
)

結果は以下になります。まずphiから。

点はMCMCサンプルの中央値で範囲は80%信頼区間です。phiは横軸:アクションのインデックス、縦軸:確率でトピックごとにプロットしています。真の値を黒の横棒で表しています。ちゃんと推定できていそうです。次はtheta。

thetaは横軸:時刻（Day）、縦軸:確率で、ユーザごとにプロットしています。色の違いはトピックの違いを表しています。各MCMCサンプルを透明度の高い折れ線で、各時刻のMCMCサンプルの中央値を点線で、データを作成した真の値を実線で書いています。時刻によってトピックの混合比、すなわち興味のあるトピックが移り変わっています。

そこそこうまく推定できていると言えるでしょうか。lambda自体はうまく推定できていませんでした。もうちょっと経験が必要そうです。ちなみに1ユーザーあたりのデータが増えていくと真の値をちゃんと推定できるようになることは確認しました。今回の計算時間は38.8mでした。

Supervised LDAとRTM（Relation Topic Model）はトピックzの実現値を使いますので、そのまま同じモデルは現状のStanではできません。代わりに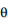を使って実装する選択肢もあるかと思います。しかし、↓（[Chang+ 2010]から引用）という理由でよくないという意見もあります（よく理解できていません）。

The issue with these formulations is that the links and words of a single document are possibly explained by disparate sets of topics, thereby hindering their ability to make predictions about words from links and vice versa.

最後にサンプルデータを作ったRのコードを載せます。

library(gtools)

T <- 31  # num of times
K <- 5   # num of topics
M <- 20  # num of users
V <- 20  # num of actions

set.seed(1234)
alpha.0.true <- rep(1, K)
alpha.pi.true <- t(apply(matrix(rep(c(0.2, 0.2, 0.2, 1, 2), M), M, K, byrow=T), 1, sample))
beta.true <- rep(0.2, V)
phi <- rdirichlet(K, beta.true)

lambda <- 1:M/400
theta <- array(0, dim=c(T,M,K))
pi <- array(0, dim=c(T-1,M,K))
theta[1,,] <- rdirichlet(M, alpha.0.true)
for(t in 2:T){
   for(m in 1:M){
      pi[t-1,m,] <- rdirichlet(1, alpha.pi.true[m,])
      theta[t,m,] <- (1-lambda[m])*theta[t-1,m,] + lambda[m]*pi[t-1,m,]
   }
}
num.word.v <- round(exp(rnorm(T*M, 5, 0.3)))

w.1 <- data.frame()
w.2 <- data.frame()
for(t in 1:T){
   for(m in 1:M){
      z <- sample(K, num.word.v[(t-1)*M+m], prob=theta[t,m,], replace=T)
      v <- sapply(z, function(k) sample(V, 1, prob=phi[k,]))
      w.1 <- rbind(w.1, data.frame(Time=t, Doc=m, Topic=z, Word=v))
      w.2 <- rbind(w.2, data.frame(Time=t, Doc=m, table(Word=v)))
   }
}
w.2$Word <- as.integer(as.character(w.2$Word))
N.1 <- nrow(w.1)
N.2 <- nrow(w.2)

offset.1 <- array(0, dim=c(T,M,2))
offset.2 <- array(0, dim=c(T,M,2))
for(t in 1:T){
   for(m in 1:M){
      r.1 <- range(which(t==w.1$Time & m==w.1$Doc))
      r.2 <- range(which(t==w.2$Time & m==w.2$Doc))
      for(i in 1:2){
         offset.1[t,m,i] <- r.1[i]
         offset.2[t,m,i] <- r.2[i]
      }
   }
}

bow <- array(0, dim=c(T,M,V))
for(n in 1:N.2)
   bow[w.2$Time[n], w.2$Doc[n], w.2$Word[n]] <- w.2$Freq[n]

save.image("input/201402_data.DTM.RData")