@dichikaさんのブログ記事でTweedie分布の存在を知りました。Stanのメーリングリストでも「推定できないの?」という質問は過去にありましたが、多忙のBobさんからは「summing out(離散値をとるパラメータの和をとって消去)すればできるかもねー」という素っ気ない返答がありました。僕でもできたので備忘録として残します。
まずTweedie分布の紹介からします。
- [1] Smyth, G. K. (1996) Regression modelling of quantity data with exact zeroes. Proceedings of the Second Australia-Japan Workshop on Stochastic Models in Engineering, Technology and Management. Technology Management Centre, University of Queensland, 572-580 (pdf file)
- [2] Wikipedia (Web)
- [3] SASのヘルプ (Web)
- [4] Rの
{twieedie}パッケージのdtweedie関数のヘルプ (Web)
密度関数の表し方やパラメータの書き方は様々あるようですが、この記事では[1]の記法を少しだけ変えた記法を使います。すなわち、、
、
([1]でいうところの
の逆数)を使って以下のように書きます(
,
,
を満たします)。

の場合は確率
で生成されます。
の場合は複合ポアソン-ガンマ分布(compound Poisson–gamma distribution)から生成されます。ガンマ分布には再生性がありますので、以下のように書くこともできます(参考記事)。

なぜではなく
に変えているかというと、ガンマ分布はscaleパラメータで指定する方法とrateパラメータで指定する方法があって、StanやBUGSではrateパラメータを使って指定し、論文ではscaleパラメータを使って指定しているからです(Wikipedia参照)。ちなみにRの
dgamma関数はどちらでも指定可能です。
Rのtweedieパッケージを使う場合は、Tweedie分布のパラメータは、
、
([1]でいうところの
)で指定します。Tweedie分布の平均の理論値は
、分散の理論値は
になります。
,
,
を満たします。なお、
、
、
と
、
、
の間には以下のような関係があります。

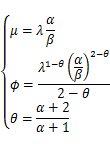
パラメータを色々試して密度関数も見ておきましょう。

上の図では見やすさのためのところだけ棒グラフにしています。Zero-inflatedな分布の一つです。特に
が1に近い場合は、ポアソン分布の離散性と分散の小さいガンマ分布の複合が効いて変態的な分布となっています。ちなみにパラメータの値は以下の通りです。
| mu | phi | theta | lambda | alpha | beta |
|---|---|---|---|---|---|
| 0.3 | 0.2 | 1.01 | 1.53 | 99 | 506.06 |
| 1 | 0.2 | 1.01 | 5.05 | 99 | 500 |
| 3 | 0.2 | 1.01 | 14.99 | 99 | 494.54 |
| 0.3 | 0.5 | 1.01 | 0.61 | 99 | 202.42 |
| 1 | 0.5 | 1.01 | 2.02 | 99 | 200 |
| 3 | 0.5 | 1.01 | 5.99 | 99 | 197.81 |
| 0.3 | 1 | 1.01 | 0.31 | 99 | 101.21 |
| 1 | 1 | 1.01 | 1.01 | 99 | 100 |
| 3 | 1 | 1.01 | 3 | 99 | 98.91 |
| 0.3 | 3 | 1.01 | 0.1 | 99 | 33.74 |
| 1 | 3 | 1.01 | 0.34 | 99 | 33.33 |
| 3 | 3 | 1.01 | 1 | 99 | 32.97 |
| 0.3 | 0.2 | 1.05 | 1.68 | 19 | 106.2 |
| 1 | 0.2 | 1.05 | 5.26 | 19 | 100 |
| 3 | 0.2 | 1.05 | 14.95 | 19 | 94.66 |
| 0.3 | 0.5 | 1.05 | 0.67 | 19 | 42.48 |
| 1 | 0.5 | 1.05 | 2.11 | 19 | 40 |
| 3 | 0.5 | 1.05 | 5.98 | 19 | 37.86 |
| 0.3 | 1 | 1.05 | 0.34 | 19 | 21.24 |
| 1 | 1 | 1.05 | 1.05 | 19 | 20 |
| 3 | 1 | 1.05 | 2.99 | 19 | 18.93 |
| 0.3 | 3 | 1.05 | 0.11 | 19 | 7.08 |
| 1 | 3 | 1.05 | 0.35 | 19 | 6.67 |
| 3 | 3 | 1.05 | 1 | 19 | 6.31 |
| 0.3 | 0.2 | 1.3 | 3.08 | 2.33 | 23.92 |
| 1 | 0.2 | 1.3 | 7.14 | 2.33 | 16.67 |
| 3 | 0.2 | 1.3 | 15.41 | 2.33 | 11.99 |
| 0.3 | 0.5 | 1.3 | 1.23 | 2.33 | 9.57 |
| 1 | 0.5 | 1.3 | 2.86 | 2.33 | 6.67 |
| 3 | 0.5 | 1.3 | 6.16 | 2.33 | 4.79 |
| 0.3 | 1 | 1.3 | 0.62 | 2.33 | 4.78 |
| 1 | 1 | 1.3 | 1.43 | 2.33 | 3.33 |
| 3 | 1 | 1.3 | 3.08 | 2.33 | 2.4 |
| 0.3 | 3 | 1.3 | 0.21 | 2.33 | 1.59 |
| 1 | 3 | 1.3 | 0.48 | 2.33 | 1.11 |
| 3 | 3 | 1.3 | 1.03 | 2.33 | 0.8 |
| 0.3 | 0.2 | 1.9 | 44.33 | 0.11 | 16.42 |
| 1 | 0.2 | 1.9 | 50 | 0.11 | 5.56 |
| 3 | 0.2 | 1.9 | 55.81 | 0.11 | 2.07 |
| 0.3 | 0.5 | 1.9 | 17.73 | 0.11 | 6.57 |
| 1 | 0.5 | 1.9 | 20 | 0.11 | 2.22 |
| 3 | 0.5 | 1.9 | 22.32 | 0.11 | 0.83 |
| 0.3 | 1 | 1.9 | 8.87 | 0.11 | 3.28 |
| 1 | 1 | 1.9 | 10 | 0.11 | 1.11 |
| 3 | 1 | 1.9 | 11.16 | 0.11 | 0.41 |
| 0.3 | 3 | 1.9 | 2.96 | 0.11 | 1.09 |
| 1 | 3 | 1.9 | 3.33 | 0.11 | 0.37 |
| 3 | 3 | 1.9 | 3.72 | 0.11 | 0.14 |
Stanで実装する際は、複合ポアソン-ガンマ分布のが離散値をとるパラメータなので、和をとって変数消去する必要があります。変数消去はたしかに面倒ですが、(Stanに限らず)推定が高速になるメリットがあります。
今回あてはめたいデータの分布と上記の密度関数の図を見比べると、Tweedie分布のパラメータthetaの値は1.3以下になりそうだと判断できたとします。すると、パラメータlambdaは15程度、すなわちMとしては1~30までを見ておけば十分によく近似できそうです。
以上よりStanで実装した例は以下になります。
- 24~25行目:
の場合は確率
で生成されます。Stanではtarget記法を使って対数確率を
targetに加えています。ベルヌーイ分布を使うこともできるでしょう。 - 27~30行目:
の場合はsumming outしてます。説明をブログでするのは面倒なので、
log_sum_exp関数については、Stan 2.9.0のマニュアルの「10. Finite Mixtures」章の「10.3. Log Sum of Exponentials: Linear Sums on the Log Scale」節を参考にしてもらえればと思います。
このモデルではmu,phi,thetaを推定してlabmda,alpha,betaを算出しています。逆に、labmda,alpha,betaをparametersブロックに置いて推定し、mu,phi,thetaをgenerated quantitiesブロックに置いて算出するモデルも試しましたが、alpha,betaがとても大きな値になる可能性があるために、これらに対する弱情報事前分布が設定できず、推定がとても遅くなりました。
データを作成して、推定を実行するRコードは以下になります。ここでは2種類のパラメータの組み合わせから乱数を生成しました。
推定結果は以下になります。
data1
| mean | se_mean | sd | X2.5. | X25. | X50. | X75. | X97.5. | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|---|---|---|
| mu | 0.97 | 0.00 | 0.07 | 0.84 | 0.92 | 0.97 | 1.02 | 1.11 | 1897 | 1.00 |
| phi | 1.00 | 0.00 | 0.10 | 0.83 | 0.94 | 1.00 | 1.07 | 1.21 | 1112 | 1.00 |
| theta | 1.31 | 0.00 | 0.04 | 1.25 | 1.29 | 1.31 | 1.34 | 1.39 | 1570 | 1.00 |
| lambda | 1.43 | 0.00 | 0.13 | 1.20 | 1.35 | 1.43 | 1.52 | 1.70 | 2036 | 1.00 |
| alpha | 2.23 | 0.01 | 0.38 | 1.57 | 1.96 | 2.20 | 2.46 | 3.06 | 1557 | 1.00 |
| beta | 3.30 | 0.02 | 0.65 | 2.25 | 2.84 | 3.24 | 3.67 | 4.83 | 1342 | 1.00 |
| lp__ | -285.97 | 0.04 | 1.28 | -289.35 | -286.54 | -285.61 | -285.05 | -284.56 | 1228 | 1.00 |
data2
| mean | se_mean | sd | X2.5. | X25. | X50. | X75. | X97.5. | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|---|---|---|
| mu | 3.02 | 0.00 | 0.06 | 2.91 | 2.99 | 3.02 | 3.06 | 3.13 | 1580 | 1.00 |
| phi | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 4000 | 1.00 |
| theta | 1.01 | 0.00 | 0.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1699 | 1.00 |
| lambda | 3.02 | 0.00 | 0.06 | 2.91 | 2.98 | 3.02 | 3.06 | 3.13 | 1613 | 1.00 |
| alpha | 94.44 | 0.11 | 4.61 | 85.56 | 91.45 | 94.33 | 97.51 | 103.69 | 1718 | 1.00 |
| beta | 94.40 | 0.11 | 4.62 | 85.51 | 91.40 | 94.29 | 97.50 | 103.56 | 1721 | 1.00 |
| lp__ | -1581.31 | 0.03 | 1.23 | -1584.42 | -1581.86 | -1580.98 | -1580.43 | -1579.94 | 1323 | 1.00 |
回帰にも少しいじれば使えると思います。