この記事はStan Advent Calendar 2016およびR Advent Calendar 2016の12月7日の記事です。StanコードとRコードは記事の最後にあります。
背景は以下です。
- [1] Aki Vehtari, Andrew Gelman, Jonah Gabry (2015). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. arXiv:1507.04544. (url)
- [2] 渡辺澄夫. 広く使える情報量規準(WAIC)の続き (注4)【WAICとクロスバリデーションの違いについて】 (url)
- [3] Sumio Watanabe. Comparison of PSIS Cross Validation with WAIC. (url)
leave-one-outクロスバリデーション(以下LOOCV)およびWAICは予測のよさをベースにしたモデル選択に用いられる情報量規準であり、ともに汎化誤差(Generalization Error、以下GE)の近似です。それにもかかわらず[1]では、本来性能評価では必須と思われる汎化誤差との比較がありません。実データ(真のモデルが未知の状況)で用いているためと思いますが、これではいけないように思います。この記事では僕が日常的に使用するような5つの基本的なモデルを使い、真のモデルが既知の状況でGE・LOOCV・WAICの性能比較を行いました。
具体的には[2]に以下のようなコメントがあります。なお[1]ではPareto Smoothed Importance SamplingでLOOCVを算出しており、PSISCVとも呼ばれるようです。
- (0) まず同じデータに対してマルコフ連鎖モンテカルロ法を何度も行ったときの値の揺らぎを調べてみましょう.WAICの分散はISCVおよびPSISCVの分散よりも小さくなります。つまり、WAICはISCVおよびPSISCVよりもマルコフ連鎖揺らぎに対して強いということができます.
- (2) しかしながら,CVもWAICも汎化誤差を推定することが本来の目的です.CVとWAICの両方の厳密値が計算できたとして,(つまりMCMC法で無限にサンプルが取れたとき),どちらの方が汎化誤差の推定として優れているのでしょうか。(中略) 我々の実験では,GEを汎化誤差とするとき,ほぼ,いつでも E[|PSISCV-GE|] > E[|WAIC-GE|] が成り立つのですが・・・。このページをご覧の皆様にはぜひ実験してみていただければと思います。なお、E[ ]は学習用データのでかたについての平均を表しています。
そこでこれら2点について検証してみました。先に「(2)のコメント」について説明します。
GE・LOOCV・WAICの比較
使用した5つのモデルとシミュレーションの手順を説明します。
重回帰
真のモデルは以下です。
あてはめたモデルは以下です。
データ点の数Nについては10,30,100,300を試しました。例としてN = 10の場合を説明します。まず乱数でデータX(すなわち)を生成します。次にその
Xの値を使って1000通りのYを生成します(学習用データのでかたの平均をとるため)。各YについてStanでiter=11000, warmup=1000, chains=4で実行して合計40000個のMCMCサンプルを得てGE・LOOCV・WAICと「LOOCV - GE」と「WAIC - GE」を求めました。その後、Nごとに「LOOCV - GE」と「WAIC - GE」のboxplotを描きました。
ロジスティック回帰
手順は重回帰の場合と同じです。使用したモデルだけが異なります。真のモデルは以下です。
あてはめたモデルは以下です。
非線形回帰 ミカエリス・メンテン型
手順は重回帰の場合と同じです。使用したモデルだけが異なります。真のモデルは以下です。
あてはめたモデルは以下です。
真のモデルが含まれない場合
あてはめたモデルが以下の場合も試しました。
ノイズがt分布に従う重回帰
手順は重回帰の場合と同じです。使用したモデルだけが異なります。真のモデルは以下です。
あてはめたモデルは以下です。
階層モデル
手順は重回帰の場合とおおよそ同じですが、データ点の数とモデルが異なります。グループの数を10に固定し、データ点の数Nについては20,50,130,400を試しました(それぞれ各グループで2,5,13,40人)。また真のモデルは以下です。
あてはめたモデルは以下です。
階層モデルにおいては何を予測したいのか(どういう状況の汎化誤差を知りたいのか)を注意深く考える必要があります。以下の記事を参照。
ここでは以下の2つの場合を計算しました。
- 既存の各グループに、新しく1人ずつ加わる場合
- 別の新しいクラスができて、新しく1人が加わる場合
結果
重回帰

大きな差はありませんでした。Nが小さい場合にWAICの方がわずかにGEに近くなる傾向があるようです。
ロジスティック回帰

大きな差はありませんでした。Nが小さい場合にLOOCVの方がわずかにGEに近くなる傾向があるようです。
非線形回帰 ミカエリス・メンテン型
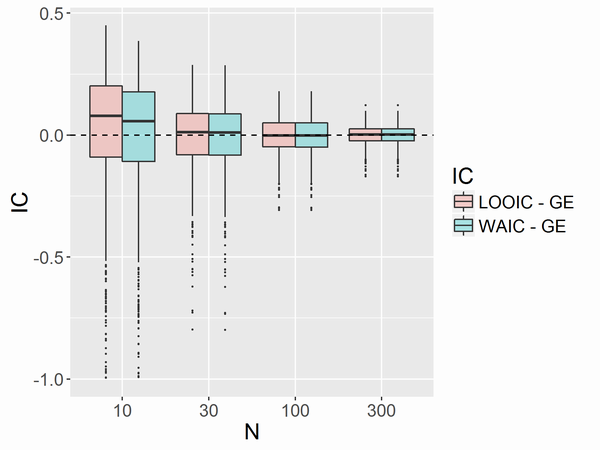
大きな差はありませんでした。Nが小さい場合にWAICの方がわずかにGEに近くなる傾向があるようです。
- 真のモデルが含まれない場合

この場合はNを増やしても汎化誤差引くエントロピー(=予測分布と真の分布のKL情報量)は0に近づかず、0.89ほどで下げ止まります。そして、Nが小さい場合にWAICの方がGEに近くなる傾向があるようです。
ノイズがt分布に従う重回帰

Nが小さい場合にWAICの方がGEに近くなる傾向があるようです。なおboxからはみ出るoutlierの値が大きく、そのままプロットすると見づらくなるので、図の縦軸を制限しました。
階層モデル
- 既存の各グループに、新しく1人ずつ加わる場合

Nが小さい場合にWAICの方がGEに近くなる傾向があるようです。
- 別の新しいクラスができて、新しく1人が加わる場合

グループ数が少ない場合、グループあたりの人数を増やしてもLOOCV - GEおよびWAIC - GEの中央値は0に近づいていきません。グループ数が少ないと、グループあたりの人数を増やしてもグループを生成する平均と標準偏差のパラメータは精度よく求められないことを反映しているのだと思います。全体的にWAICの方がわずかにGEに近くなる傾向があるようです。
階層モデル その2 2016.12.14追記
伊庭先生から以下のような要望がありました。
WAICと汎化誤差の比較,グループ数固定だけでなく,グループごとのサンプルサイズ一定の極限(グループ数もサンプルサイズも比例して同時に増える)でもやってみてほしいです.状態空間モデルや平滑化などの場合は各時点での観測数一定が自然 https://t.co/qkRrB0TS4A
— baibai (@ibaibabaibai) 2016年12月7日
理論と比較する場合は (A)何を予測したいのか(どういう状況の汎化誤差を知りたいのか【元ブログのより】(B)どういう極限をとるのか,の両方が絡んでくると思います. https://t.co/1jZDKNJlnn
— baibai (@ibaibabaibai) 2016年12月7日
そこでモデルは同じものを用いて、グループあたりの人数を固定し(2,5,13のうちいずれか)、グループの数が10,30,100の各場合で実行してみました。
- 既存の各グループに、新しく1人ずつ加わる場合
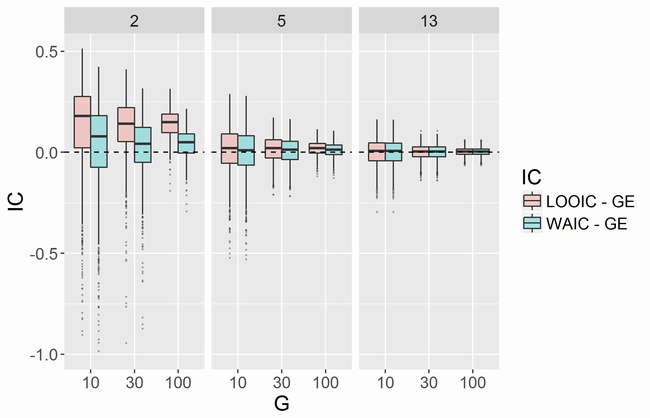
グループあたりの人数が少ない場合、グループ数を増やすとLOOCV - GEおよびWAIC - GEのバラツキは少なくなるもの、それらの中央値は0に近づいていきません。グループ数を増やしても各グループには2人しかいないため、グループごとの予測はあたらないままということを反映しているのだと思います。グループあたりの人数が小さい場合にWAICの方がGEに近くなる傾向があるようです。
- 別の新しいクラスができて、新しく1人が加わる場合

Gが小さい場合にWAICの方がわずかにGEに近くなる傾向があるようです。
* * *
5つのモデルを通して見ると、Nが小さい場合、すなわち1サンプルの重みが大きい場合にはWAICのほうがLOOCVよりもよい汎化誤差の近似になっているようです。[2]の「PSISCVとWAIC:実験例 追加」によると、影響の大きい(重みの大きい)サンプルが存在する場合にも同じような結果になるようです。以下の伊庭先生のツイートはこのような状況を指していると思われます。
MCMCで事後分布を計算するとき,1個のサンプルの部分の尤度(独立サンプルを過程)の逆数で重みをつけて計算すればleave-oneしたことになるから,いろいろ抜いたのが一回のRUNでできるわけ.しかしこれ,1個抜いてある程度大きく変わる場所を抜いたら不味いことになりそう. https://t.co/uLWMbeAAZy
— baibai (@ibaibabaibai) 2016年10月22日
WAICはLOOCVよりMCMCの揺らぎに強いか?
次に「(0)のコメント」について検証しました。前述の5つのモデルに対し、Nを10または100とし、各Nについてデータを5通り生成しました。さらに各データセットに対して、MCMCのシードを1000通り試し、1000個のLOOCVとWAICを求め、それぞれの分散と平均と変動係数を求めました。
結果
いずれの場合についても実用上の差が認められませんでした。Nが100の場合より10の場合の方がMCMCの揺らぎがありますが、それでも変動係数にして高々1%程度でした。なお、この結果はMCMCサンプルを求めるアルゴリズムの違いやMCMCサンプルの数にも依存すると思います。
まとめ
Nが大きい場合には、WAICとLOOCVにほぼ差がないと言えるでしょう。Nが小さい場合には、WAICの方が汎化誤差のよい近似になっていると言えるでしょう。- さらに理論的な美しさや計算速度も含めて総合的に判断すると、WAICに軍配が上がると思います。
おまけ
データとは異なる
における
の予測分布
を考えたい場合があると思います。その場合は、一般によい情報量規準があるか未解明で、研究対象として興味深いようです(渡辺澄夫先生(私信))。例えば単回帰の場合には、真のモデルがあてはめたモデルに含まれており、かつモデルに依存する量を使うと情報量規準に準ずる量を構築できるようです。興味深いです。
ソースコード
「(2)のコメント」を検証するための、重回帰の場合と階層モデルの場合のStanコードとRコードを公開します。
重回帰
Stanコード
重回帰のモデルの部分は「StanとRでベイズ統計モデリング」の9.2.1項と同じです。異なる点はgenerated quantitiesブロックでGE・LOOCV・WAICを算出するためにlog_likとy_predを算出している点です。
Rコード
例としてNが100の場合を載せます。理解しやすさのため、並列化していないコードにしてありますが、実際には色々並列化して計算しています。
- 16~17行目: 学習用データの出かたの平均をとりたいので、データ
Yを乱数で生成しています。 - 22~31行目: データごとのエントロピーと汎化誤差を計算しています。以前の記事参照。このコードのように十分なMCMCサンプルから予測分布の近似関数を求めて汎化誤差を算出する方法のほか、直接MCMCサンプルを使って求める方法もあるかと思います(渡辺先生はそうしています)。
- 23~24行目: 予測分布は滑らかだと仮定し、40000個のMCMCサンプルから予測分布の密度関数を計算しています。Rのデフォルトの
density関数よりも{KernSmooth}パッケージのbkde関数の方が優秀っぽいのでこちらを使っています(参考pdf)。 - 25行目: 真の分布です。
- 26行目: エントロピーの計算の際に積分される関数です。
- 27行目: 汎化誤差の計算の際に積分される関数です。予測分布の密度推定した結果を
approxfunで関数に変換している関係上、f_predがごくまれに絶対値の小さな0以下の値を返します。それを避けるためにifelse関数をかませてあります。 - 28~29行目: それぞれエントロピーと汎化誤差を計算しています。ここでは
f_trueは正規分布なので、-6SD~+6SDまで積分すれば十分よい近似となります。Rのデフォルトのintegrate関数はちょっと賢くてadaptiveに積分しているので計算は早いのですが、まれに不安定で計算ができない場合があります。そのため、少し遅いですが安定な数値積分の手法であるRombergの方法を使っています({pracma}パッケージのromberg関数または{Rmpfr}パッケージのintegrateR関数を使うことができます)。 - 34行目: 汎化誤差(GE)のサンプルに関する平均を求めています。学習用データと同じ
NとXの値を持つ新しいデータセットに対して予測を行い、1サンプルあたりの汎化誤差を求めていることに相当します。 - 35~36行目: Stanのチームが開発している
{loo}パッケージを用いてlooicとwaicを求めています。彼らの情報量規準のスケールはAICやDICとあわせて倍となっているので、1サンプルあたりにスケールをあわせる意味で
2*Nで割っています。
階層モデル「既存の各グループに、新しく1人ずつ加わる場合」
階層モデルの場合のWAICの詳しい解説は以前の記事を参照してください。
Stanコード
Rコード
重回帰の場合と似ています。
- 23~32行目: グループ
gに1人加わった場合の汎化誤差error_by_groupを求めています。重回帰の場合にサンプルごと(nごと)だったのが、グループごと(gごと)にインデックスが変わっただけで、内容は変わっていません。 - 35行目: 「既存の各グループに、新しく1人ずつ加わる場合」なので、各グループの汎化誤差の和になります。
- 36~37行目: 各グループごとにLOOCVまたはWAICを求めて和をとっています。
階層モデル「別の新しいクラスができて、新しく1人が加わる場合」
Stanコード
Rコード
- 25~26行目: この場合は真の分布が積分を含んでいるので少し複雑です。
残りは「既存の各グループに、新しく1人ずつ加わる場合」とほぼ同じです。
なお、この記事は以下のツイートによってやってみようかなと思いました。
#数楽 予測誤差を測るための各種情報量規準の正しい比較の例が https://t.co/A9N31GtCH6 の注4にあります。ソースも公開で素晴らしい。しかしMatlabには一般人は高価なので手が出ない。RStanで検証するためのコードを誰か公開すると社会貢献になると思う。
— 黒木玄 Gen Kuroki (@genkuroki) 2016年10月27日