{Rcpp}と{RcppGSL}を活用した数値積分の例
GSLはGNU Scientific Libraryの略で, 広い用途の数値計算向けのC言語のライブラリです。20年前から開発されており、まだリリースされ続けています。個人的な印象としては、めちゃくちゃチューニングされてはいないが、長年の開発のおかげで安定しており、マニュアル(htmlはこちら、pdfはこちら)も充実していて使いやすいイメージです。
この記事では{Rcpp}と{RcppGSL}パッケージを通してRからGSLを使う例(数値積分)を挙げます。このような{Rcpp}を使って数値計算を行う類似パッケージには{RcppNumerical}が挙げられます。
なお、RからC++を使うためのパッケージである{Rcpp}自体の解説はしません。{Rcpp}の使い方とメリットに関しては、最近非常によい本が出版されました。以下の本の24章を参照するとよいと思います。
インストール
GSLのインストール
Linuxの場合
僕の動作環境はRは3.3.1、gccは6.1.1、gslは2.3です。
パッケージマネージャのようなものからインストールすることもできますが、僕は諸事情でソースからインストールしました。Linuxで典型的な手順を踏めばインストールできます。例えば、公式ページからtar.gzをダウンロードして、解凍してconfigure、make、make installしてしばらく待ちます。
その後、.bashrcなどで「gslをインストールしたディレクトリ」を以下のように環境変数LD_LIBRARY_PATHに追加しておきます。
export LD_LIBRARY_PATH=".:「gslをインストールしたディレクトリ」/lib:$LD_LIBRARY_PATH"
Macの場合
持ってないので分かりません。すみません。
Windowsの場合
僕の動作環境はRは3.3.1、RtoolsはRtools33またはRtools34です。
最新版のGSLでなくてもよければ、Ripley先生が提供しているサイトから、Windows用にprebuildされたGSL(local323.zip)をダウンロードして、、、と思ったら、先週ぐらいから403 Forbiddenになっているようです。終了です。*1Ripley先生が退職されたあとも今まで残っていたのが奇跡なのかもしれません。Cygwinからだとインストールできるかもですが、Rtoolsとの連携もしんどそうで頑張る元気がありません。素直にLinuxかMacを使った方がよさそうです。
{Rcpp}と{RcppGSL}のインストール
いつも通りでOKです。すなわち、Rを起動してinstall.packages(c('Rcpp', 'RcppGSL'))でいけます。
テスト
テスト用のコードは作者のページにあるものを使います。C++ファイルとしてtest0.cppというファイル名で以下の内容で保存します。[[Rcpp::depends(RcppGSL)]]に注意です。
// [[Rcpp::depends(RcppGSL)]] #include <RcppGSL.h> #include <gsl/gsl_matrix.h> #include <gsl/gsl_blas.h> // [[Rcpp::export]] Rcpp::NumericVector colNorm(const RcppGSL::Matrix & G) { int k = G.ncol(); Rcpp::NumericVector n(k); for (int j = 0; j < k; j++) { RcppGSL::VectorView colview = gsl_matrix_const_column(G, j); n[j] = gsl_blas_dnrm2(colview); } return n; }
さらに、別途Rファイルとしてtest0.Rというファイル名で以下の内容で保存します。
library(Rcpp) library(RcppGSL) sourceCpp('test0.cpp') set.seed(123) m <- matrix(rnorm(4), ncol=2) print(colNorm(m)) #=> 0.6059 1.5603
Rコンソールを起動してそのディレクトリに移動し、source('test0.R')を実行して無事に0.6059 1.5603が出力されれば完了です(小数点何位まで出力されるかはRのオプションの指定によって異なると思います)。
RcppGSL活用例:数値積分
Rに数値積分するintegrate関数があるのに、わざわざ自分で数値積分を書くバカがどこにおるの?と思われるかもしれませんが、近頃おじさんはRのintegrate関数が機能しない場面にしょっちゅう出くわします。例を挙げます。
ここで、と
は値が与えられています。例えば、
とし、
を
から
の間のいくつか選んで算出してみます。数値積分の範囲は
から
まできちんと計算しなくても、
から
までの積分でほぼ十分とします。
Rだけで算出する場合は以下になります。
sd <- 0.24 integrand <- function(x, mu) (0.2 + min(x, -0.3-x)) * dnorm(x, mean=mu, sd=sd) g1 <- function(mu) integrate(integrand, mu-6*sd, mu+6*sd, mu)$value g2 <- function(mu) pracma::romberg(integrand, a=mu-6*sd, b=mu+6*sd, mu=mu)$value x <- seq(-3, 3, len=101) m1 <- sapply(x, g1) m2 <- sapply(x, g2)
g1はintegrate関数で、g2は比較ためのRomberg法で数値積分した結果です。{pracma}パッケージのromberg関数で実行できます。この結果を可視化すると以下になります。
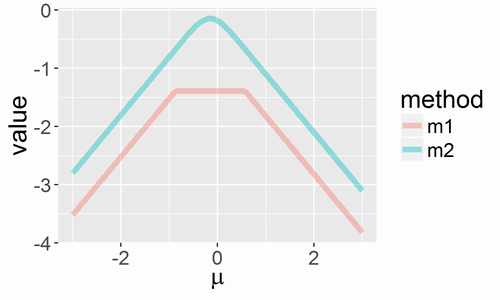
値がだいぶずれていますが、romberg関数の方が正しい値です。それならばromberg関数をいつも使えばいいじゃんと思うかもしれませんが、計算に時間がかかるのと、ここでは挙げませんがromberg関数だとかえって数値計算がうまくいかない場合もあります。そこで、{RcppGSL}パッケージからで数値積分します。
テストの場合と同様に、C++ファイルとしてgsl_cquad.cppというファイル名で以下の内容で保存します。
// [[Rcpp::depends(RcppGSL)]] #include <RcppGSL.h> #include <gsl/gsl_integration.h> #include <gsl/gsl_randist.h> struct my_f_params { double mu; double sd; }; double integrand(double x, void *p) { struct my_f_params * params = (struct my_f_params *)p; double mu = params->mu; double sd = params->sd; double res = (0.2 + fmin(x, -0.3-x)) * gsl_ran_gaussian_pdf(x-mu, sd); return(res); } // [[Rcpp::export]] Rcpp::NumericVector integrate_my_cquad(Rcpp::NumericVector xVec, double sd) { Rcpp::NumericVector resVec(xVec.size()); gsl_integration_cquad_workspace *work = gsl_integration_cquad_workspace_alloc(1e2); double result(0.0); double abserr(0.0); size_t nevals(1e2); double mu(xVec[0]); gsl_function F; F.function = &integrand; struct my_f_params params = { mu, sd }; for (int i=0; i < xVec.size(); ++i) { mu = xVec[i]; params.mu = mu; F.params = ¶ms; int res = gsl_integration_cquad(&F, mu-6*sd, mu+6*sd, 1e-8, 1e-6, work, &result, &abserr, &nevals); resVec[i] = result; } gsl_integration_cquad_workspace_free(work); return resVec; }
- 3行目: GSLの数値積分の機能を使用する場合に必要となるヘッダーファイルです。
- 4行目: GSLの確率分布を使用する場合に必要となるヘッダーファイルです。
- 8~14行目: 被積分関数です。
xが積分変数で、pはその他の変数(パラメータ)です。RcppGSLで数値積分する場合、被積分関数はR側で作って渡すのではなく、C++側で定義しないと高速にならないので注意です。なお、gsl_ran_gaussian_pdfは正規分布の確率密度関数です。 - 6行目: いま説明した
pに値を渡すための構造体です。 - 17~40行目: 数値積分を実行する自作関数を定義しています。Rの
vectorがxVecに渡され、そのxVecの各値ごとに数値積分を繰り返し実行して、その結果をRのvectorとなるresVecで返します。数値積分にもいろいろ手法があります。特異点がある場合にRのintegrate関数がこける印象があることから、QAGSとCQUADを検討した結果、CQUADの方が安定で速いケースが多かったので、この記事ではCQUADを使います。 - 34行目:
gsl_integration_cquadは数値積分をCQUADで実行する関数です。引数の説明についてはマニュアルを参照してください。引数の一つであるworkは作業領域になります。19行目のgsl_integration_cquad_workspace関数でその領域を確保し、38行目のgsl_integration_cquad_workspace_free関数でその領域を開放します。
C++ファイルで定義したintegrate_my_cquadを使うRスクリプトは以下になります。
library(Rcpp) library(RcppGSL) sourceCpp('gsl_cquad.cpp') sd <- 0.24 x <- seq(-3, 3, len=101) m3 <- integrate_my_cquad(x, sd)
計算の実行速度は非常に速く、また安定で、結果も上記のRomberg法とほぼ一致します。僕の実行環境で1000回ほどintegrate_my_cquad関数と同じ処理をして比較したところ、GSL版はRのromberg関数の約150倍、Rのintegrate関数の約1.5倍高速でした。
*1:portingのページはかろうじて残っていますが、、
