スパースモデルではshrinkage factorの分布を考慮しよう　～馬蹄事前分布（horseshoe prior）の紹介～

ベイズ統計の枠組みにおいて、回帰係数の事前分布に二重指数分布（ラプラス分布）を設定し回帰を実行してMAP推定値を求めると、lassoに対応した結果になります。また、回帰係数にt分布を設定する手法もあります。これらの手法は「shrinkage factorの分布」という観点から見ると見通しがよいです。さらに、その観点から見ると、馬蹄事前分布が魅力的な性質を持っていることが分かります。この記事ではそれらを簡単に説明します。

なお、lassoそのものに関しては触れません。岩波DS5がlassoを中心にスパースモデリングを多角的に捉えた良い書籍になっているので、ぜひそちらを参照してください。

岩波データサイエンス Vol.5

発売日: 2017/02/16
メディア: 単行本（ソフトカバー）

参考文献

[1] C. Carvalho et al. (2008). The Horseshoe Estimator for Sparse Signals. Discussion Paper 2008-31. Duke University Department of Statistical Science.　(pdf file)
[2] J. Piironen and A. Vehtari (2016). On the Hyperprior Choice for the Global Shrinkage Parameter in the Horseshoe Prior. arXiv:1610.05559. (url)
[3] C. Carvalho et al. (2009). Handling Sparsity via the Horseshoe. Journal of Machine Learning Research - Proceedings Track. 2009;5:73–80. (pdf file)
[4] Epistemology of the corral: regression and variable selection with Stan and the Horseshoe prior：PyStanの開発者による、PyStanでの実装例とlassoとの比較です。

horseshoe+ priorなんてのも提案されています。

理論編

分割された正規分布

まず分割された正規分布の復習から。例えば、PRMLの2.3.2項に記述があります。以下の多変量正規分布があるとします。

f:id:StatModeling:20201106171132p:plain

ここで、以下のように2つに分割します。

f:id:StatModeling:20201106171136p:plain

f:id:StatModeling:20201106171141p:plain

f:id:StatModeling:20201106171145p:plain

すると条件付き分布は以下になります。

f:id:StatModeling:20201106171148p:plain

f:id:StatModeling:20201106171153p:plain

shrinkage factorの導出

上記の[2]を参考にしました。丁寧な導出が見つからなかったので、以下は手計算で求めました。間違っていましたら連絡ください。

以下の線形モデルを考えます。

f:id:StatModeling:20201106171157p:plain

ここで $\overrightarrow{\beta}$ が回帰係数のベクトルで $\bf{X}$ が説明変数の行列です。多変量正規分布で表現すると以下になります。

f:id:StatModeling:20201106171202p:plain

ここで、 $\bf{\Lambda}$ は以下の対角行列です。

f:id:StatModeling:20201106171205p:plain

　＊　＊　＊

さて、ここで以下の $\overrightarrow{z}$ を考えます。

f:id:StatModeling:20201106171209p:plain

同時分布の対数は以下になります。

f:id:StatModeling:20201106171213p:plain

これは $\overrightarrow{z}$ の要素の2次関数なので、 $p(\overrightarrow{z})$ も正規分布になります。PRMLの2.3.3項とほぼ同じように、2次の項と1次の項にわけて考えることで、その正規分布の精度行列と平均ベクトルを求めることができます。まずは2次の項を整理すると、

f:id:StatModeling:20201106171217p:plain

f:id:StatModeling:20201106171221p:plain

となり、精度行列 $\bf{T}$ が求まります。1次の項はないので、平均ベクトルは以下になります。

f:id:StatModeling:20201106171226p:plain

以上より、前述の「分割された正規分布」の公式より、 $\overrightarrow{y}$ が与えられたもとでの $\overrightarrow{\beta}$ の分布は以下になります。

f:id:StatModeling:20201106171229p:plain

ここで、平均ベクトルは以下のように計算できます。

f:id:StatModeling:20201106171234p:plain

f:id:StatModeling:20201106171239p:plain

f:id:StatModeling:20201106171242p:plain

f:id:StatModeling:20201106171246p:plain

ここで、 $\overrightarrow{\hat{\beta}}$ は $\overrightarrow{\beta}$ の分布を考えない場合の最尤推定の解で以下です。

f:id:StatModeling:20201106171249p:plain

　＊　＊　＊

さて、ここで各説明変数列が相関がなく、平均がゼロで、分散が1とします。すなわち、以下を仮定します。

f:id:StatModeling:20201106171252p:plain

すると、平均ベクトルは以下のように変形できます。

f:id:StatModeling:20201106171256p:plain

f:id:StatModeling:20201106171300p:plain

対角行列になるので要素ごと表すと、以下になります。

f:id:StatModeling:20201106171304p:plain

ここで、 $\kappa_j$ は以下となり、shrinkage factorと呼ばれます。

f:id:StatModeling:20201106171307p:plain

shrinkage factorが0に近いと係数が最尤推定値に近くなり（shrinkageしてない）、1に近いと0に近くなります（shrinkageする）。

馬蹄事前分布（horseshoe prior）

上のモデルで各 $\lambda_j$ がある確率分布に従うと仮定します。この確率分布によって、元の $\beta_j$ にどんな確率分布を設定したのと等価になるのか、そしてshrinkage factorの分布がどのようになるのか手計算で求めることができます（参考：確率変数の変数変換とヤコビアンに慣れる - StatModeling Memorandum）。以下に結果だけ対応表として載せておきます（手計算で求めましたが間違っていたらすみません）。

手法名	$\beta_j$ の分布	$\lambda_j$ の分布
lasso	double-exponential
-	Student-t*1
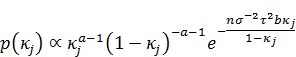horseshoe		*2

shrinkage factor（ $\kappa_j$ ）の分布を描くと以下になります。

f:id:StatModeling:20201106171128p:plain

horseshoeの場合の $\kappa_j$ の分布形が馬蹄に似ているので馬蹄事前分布（horseshoe prior）と名づけられました。なお、 $n \sigma^{-2} \tau^{2} = 1$ のときはベータ分布 Beta(0.5, 0.5) に一致します。

馬蹄事前分布のようにshrinkage factorが0か1を生成しやすいということは、「0につぶしやすい一方で、0につぶれない係数は0に近づくような振る舞いをしないで最尤推定値に近づく」ことになります。係数にメリハリがあるわけです。これに対し、lassoの場合は $n \sigma^{-2} \tau^{2}$ が1もしくは10だとあまり0につぶす傾向はなく、またつぶれなかった係数は少しだけ最尤推定値に近づく感じになります。 $n \sigma^{-2} \tau^{2} = 0.1$ だと0につぶす傾向はあるのですが、つぶれなかった係数も0に近づけてしまいます。

この結果、C. Carvalhoらはシミュレーション実験から「一部だけ影響のない説明変数があるようなシミュレーションデータに対しては馬蹄事前分布の方が予測の性能がよい」と主張しています（[3]）。さらに馬蹄事前分布は二重指数分布（ラプラス分布）とは異なり至るところで微分可能なので、偏微分を使うStanでの推定が安定であることから、Stanの開発メンバーはスパースモデリングには二重指数分布よりも馬蹄事前分布の使用をすすめています。

Stanによる実装例

[4]の実装に尽きています。すなわち以下です。簡単です。

data {
  int<lower=0> N;
  int<lower=0> D;
  matrix[N,D] X;
  vector[N] Y;
}

parameters {
  vector[D] beta;
  vector<lower=0>[D] lambda;
  real<lower=0> tau;
  real<lower=0> sigma;
}

model {
  lambda ~ cauchy(0, 1);
  tau ~ cauchy(0, 1);
  for (d in 1:D)
    beta[d] ~ normal(0, lambda[d] * tau);
  Y ~ normal(X * beta, sigma);
}

Enjoy!

*1:参考： http://stats.stackexchange.com/questions/52906/student-t-as-mixture-of-gaussian

*2:正の部分だけ定義された半コーシー分布