トピックモデルシリーズ 4 LDA （Latent Dirichlet Allocation）

このシリーズのメインともいうべきLDA（[Blei+ 2003]）を説明します。前回のUMの不満点は、ある文書に1つのトピックだけを割り当てるのが明らかにもったいない場合や厳しい場合があります。そこでLDAでは文書を色々なトピックを混ぜあわせたものと考えましょーというのが大きな進歩です。さてこの記事の表記法は以下になります。前回のUMの場合と同一です。

右2列は定数については数値を、そうでないものについてはR内の変数名を書いています。データは前の記事参照。 グラフィカルモデルは以下になります（左: LDA, 右（参考）: 前回のUM）。

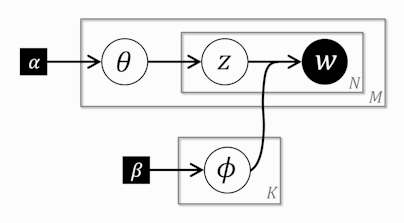
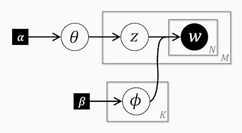
見ると四角のプレートが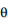まで伸びてきただけです。しかしながらこれが曲者でUMからかなりのギャップがあります。以下の吹き出しの順に説明していきます。

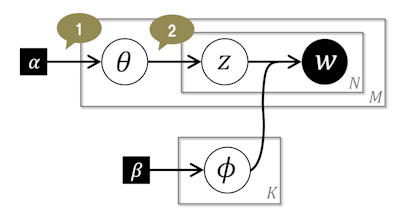
①

ここではハイパーパラメータからディリクレ分布に従って『文書の数だけ』が生成されます。このは以下のような『文書内の単語ごとの』トピックを決める、いびつなK面サイコロです。文書ごとに形が変わります。NB, UMの時は階層がひとつ上で、サイコロは1つで『文書ごとの』トピックを決めていたことを思い出してください。LDAのも「トピック分布」と呼ばれます。しかしながら文書内のトピックの構成比を決めますので、これを強調するために「トピック混合比」とも呼ばれます。トピック混合比が決まれば文書内の単語の構成比はおおまかに決まります。

②

ある文書内の『単語ごとに』トピックを決めます。文書が変わるとトピックを決めるサイコロが変わります。

残りはNB, UMと同じです。まとめますと以下の図のようになります。

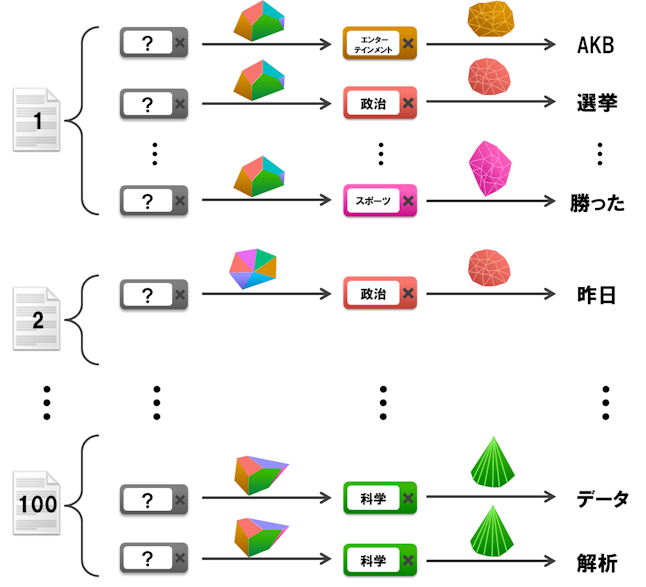
UMから上記のモデルに変わったことで柔軟性が大幅に向上します。そして未知の文書が与えられた時に、途中まで読んで文書のトピック混合比を推定することで、以降の単語の出現予測の精度が飛躍的に高まります。別の視点から見ると、LDAがやっていることは、文書の特徴を大きな単語次元（V）から小さなトピック次元（K）に圧縮していることに相当します。文書の特徴はトピック混合比であるになります。LDAの結果、単語をクラスタリングすることもできますし、文書をクラスタリングすることもできます。実例としましてはSmartNews開発者ブログさまのこの記事がイメージしやすくて分かりやすいです。

次にStanでの実装にうつります。まずはイメージしやすいようにStanがいつか離散パラメータを許してくれた時のStanコードを示します。

data {
   int<lower=1> K;                    # num topics
   int<lower=1> M;                    # num docs
   int<lower=1> V;                    # num words
   int<lower=1> N;                    # total word instances
   int<lower=1,upper=V> W[N];         # word n
   int<lower=1,upper=N> Offset[M,2];  # range of word index per doc
   # hyperparameter
   vector<lower=0>[K] Alpha;     # topic prior
   vector<lower=0>[V] Beta;      # word prior
}
parameters {
   simplex[K] theta[M];        # topic dist for doc m
   simplex[V] phi[K];          # word dist for topic k
   int<lower=1,upper=K> z[N];  # FUTURE: topic index for word n
}
model {
   # prior
   for (m in 1:M)
      theta[m] ~ dirichlet(Alpha);
   for (k in 1:K)
      phi[k] ~ dirichlet(Beta);

   # likelihood
   for (m in 1:M) {
      for (n in Offset[m,1]:Offset[m,2]) {
         z[n] ~ categorical(theta[m]);
         W[n] ~ categorical(phi[z[n]]);
      }
   }
}

しかしながら、15行目が現状ではNGです。この『単語ごとの』トピックzが離散パラメータなのでsumming outしなくてはなりません。前回同様、文書ごとに独立と考えられるので、ある1つの文書mだけを考えます。そして、その『文書m内の』『ある1つの』単語の出現確率は、トピック1の目が出たとしてトピック1のサイコロからある単語が作られた確率＋トピック2の目が出たとしてトピック2のサイコロからある単語が作られた確率＋...＋トピックKの目が出たとしてトピックKのサイコロからある単語が作られた確率 の和になります。これがすべての単語の分だけありますので、単語分の積になります。これを数式で書くと以下になります。

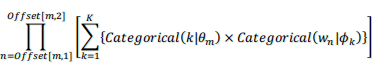
このlogをとったものが『文書mの』log probabilityの増加分になります。以下のようになります（式変形については前回のlog_sum_exp()の説明を参照）。

最後に文書mのmを1～M回まで繰り返せばOKです。実際のStanの実装は以下のようになります。

data {
   int<lower=1> K;                    # num topics
   int<lower=1> M;                    # num docs
   int<lower=1> V;                    # num words
   int<lower=1> N;                    # total word instances
   int<lower=1,upper=V> W[N];         # word n
   int<lower=1,upper=N> Offset[M,2];  # range of word index per doc
   # hyperparameter
   vector<lower=0>[K] Alpha;     # topic prior
   vector<lower=0>[V] Beta;      # word prior
}
parameters {
   simplex[K] theta[M];   # topic dist for doc m
   simplex[V] phi[K];     # word dist for topic k
}
model {
   # prior
   for (m in 1:M)
      theta[m] ~ dirichlet(Alpha);
   for (k in 1:K)
      phi[k] ~ dirichlet(Beta);

   # likelihood
   for (m in 1:M) {
      for (n in Offset[m,1]:Offset[m,2]) {
         real gamma[K];
         for (k in 1:K)
            gamma[k] <- log(theta[m,k]) + log(phi[k,W[n]]);
         increment_log_prob(log_sum_exp(gamma));
      }
   }
}

• 26行目：gammaはlog_sum_exp()の引数になるarrayです。
• 28行目：theta[m,k]はのことです。log(.)の代わりにcategorical_log(k,theta[m])でもOKです。phi[k,W[n]]はのことです。log(.)の代わりにcategorical_log(W[n],phi[k])でもOKです。
• 29行目、log probabilityの増加分はincrement_log_prob()を使ってStanに教えてあげます。結局StanではデータからK面サイコロtheta（M個）、V面サイコロphi（K個）の形を推定することになります。

これをキックするRのコードは以下になります。

library(rstan)

load("input/201402_data1.RData")

data <- list(
   K=K,
   M=M,
   V=V,
   N=N.1,
   W=w.1$Word,
   Offset=offset.1,
   Alpha=rep(1, K),
   Beta=rep(0.5, V)
)

fit <- stan(
   file='model/LDA.stan',
   data=data,
   iter=1000,
   chains=1,
   thin=1
)

今までは分かりやすさを重視させるためデータの形としてはw.1（前の記事参照）を使ってきましたが、高速化のため今からw.2を使います。結果は変わりません。w.1ではある文書内に同じ単語が出てくると別の行になっていたため、その分全く同じ計算が繰り返されていましたが、単語の出現回数（Freq）を使うようにすることで繰り返す部分が掛け算になります。表記法は以下のように変わります。

Stanの実装は以下になります。

data {
   int<lower=2> K;                    # num topics
   int<lower=2> V;                    # num words
   int<lower=1> M;                    # num docs
   int<lower=1> N;                    # total word instances
   int<lower=1,upper=V> W[N];         # word n
   int<lower=1> Freq[N];              # frequency of word n
   int<lower=1,upper=N> Offset[M,2];  # range of word index per doc
   vector<lower=0>[K] Alpha;          # topic prior
   vector<lower=0>[V] Beta;           # word prior
}
parameters {
   simplex[K] theta[M];   # topic dist for doc m
   simplex[V] phi[K];     # word dist for topic k
}
model {
   # prior
   for (m in 1:M)
      theta[m] ~ dirichlet(Alpha);
   for (k in 1:K)
      phi[k] ~ dirichlet(Beta);

   # likelihood
   for (m in 1:M) {
      for (n in Offset[m,1]:Offset[m,2]) {
         real gamma[K];
         for (k in 1:K)
            gamma[k] <- log(theta[m,k]) + log(phi[k,W[n]]);
         increment_log_prob(Freq[n] * log_sum_exp(gamma));
      }
   }
}

8行目が追加され、29行目が少し変更されただけです。単語の出現回数の分だけnのループで繰り返されていたのが掛け算に変更されました。

これをキックするRのコードは以下になります。

library(rstan)

load("input/201402_data1.RData")

data <- list(
   K=K,
   M=M,
   V=V,
   N=N.2,
   W=w.2$Word,
   Freq=w.2$Freq,
   Offset=offset.2,
   Alpha=rep(1, K),
   Beta=rep(0.5, V)
)

fit <- stan(
   file='model/LDA.Freq.stan',
   data=data,
   iter=1000,
   chains=1,
   thin=1
)

9-12行目が変更点です。

結果は以下になりました。まずは1文書あたりの総単語数が少ない場合（data1; 20単語程度）から。thetaとphiは以下の通りです。

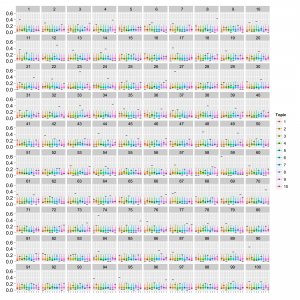
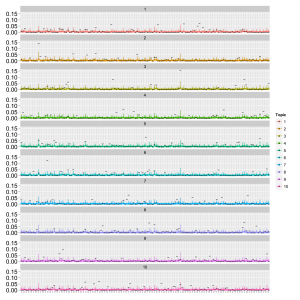
点はMCMCサンプルの中央値で範囲は80%信頼区間です。thetaは横軸:トピックのインデックス、縦軸:確率で、文書ごとにプロットしています。phiは横軸:単語のインデックス、縦軸:確率でトピックごとにプロットしています。真の値を黒の横棒で表しています。phiの値がトピックが違っていてもほとんど同じような値に収束していることが分かります。これはデータが少なくてトピックの分離がうまくできていないと予想されます。MCMCサンプリングですと混合ガウス分布の推定でも似たような状況になります。次に1文書あたりの総単語数が多い場合（data2; 150単語程度）。thetaとphiは以下の通り。

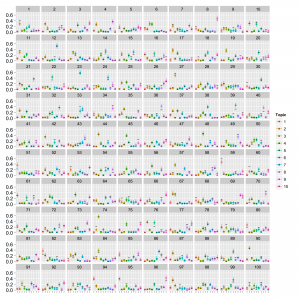
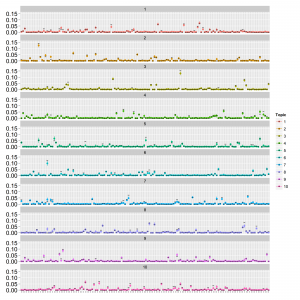
バッチリうまくいっています。見てきたようにデータ数によって結果が大きく変わりますので、収束したかどうかだけでなく導き出された結果がreasonableかどうかをちゃんと検証することが重要になります。

モデルのパラメータ数（Stanで出力される数です。ホントはsimplexの制限があるので実質的な数は少し減ります）や推定にかかった計算時間などは以下の通りです。

項目	文書あたりの単語数	NB	UM	LDA	LDA(Freq)	PAM	GaP
パラメータ数	少/多	1450	1450	2440	2440	？	？
計算時間	少	5.5m	2.3m	7.7m	7.4m	？	？
収束具合	少	○	×	○	○	？	？
lp__	少	-13892	-13882	-16920	-16919	？	？
計算時間	多	30.8m	11.7m	53.7m	30.4m	？	？
収束具合	多	○	○	○	○	？	？
lp__	多	-74154	-75760	-76793	-76787	？	？

現状ではStanによるLDAは文書数x単語の種類が2000x2000ぐらいまでで、データが十分の場合には実用に足るかなと思っています。他の実装と比べた時の長所は、最尤推定ではなくHMCサンプリングによる推定の正確さとモデルの拡張のしやすさです。スモールデータをお持ちの方は試してみてはいかがでしょうか。モデルの拡張もしないでLDAそのものをやるだけなら良い実装がいくつか転がっていますのでそれらを使った方が実行速度が圧倒的に速くていいと思います。