トピックモデルシリーズ 6 GaP （Gamma-Poisson Model）

この記事の表記は以下です。Wがbag-of-wordsの行列を表すことに注意してください。

右2列は定数については数値を、そうでないものについてはR内の変数名を書いています。データは前の記事参照。

LDAの記事で、『別の視点から見ると、LDAがやっていることは、文書の特徴を大きな単語次元（V）から小さなトピック次元（K）に圧縮していることに相当します』と書きました。少し一般化して考えますと、LDAとはM×Vの行列であるW（bag-of-words）を、M×K行列である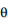とK×V行列であるに分ける、discrete PCAの一種とみなすことができます。componentの数がKになります。[Buntine+ 2005]では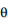をcomponent score matrix、をcomponent loading matrixと呼んでいるので以下ではそれにならうことにします。

LDAでは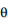は多項分布（K面サイコロ）であり、合計値が1という制限がありました。この制限をはずして正の値ならなんでもOKにしたものがGaPになります。LDAと比べて使用するメモリの量は増えますが、上記の制限をはずすことで例えば、「文書全体を見て最もトピック1に高いscoreを持っている文書はどれか」などを得ることが可能になります。またbag-of-wordsをデータとして使っているので文書あたりの総単語数が多い時も計算時間があまり増えないメリットがあります。統数研の講座では持橋先生が「GaPは性能もかなりよく、企業の人ならこちらがオススメかも」とおっしゃっていました。

グラフィカルモデルは以下になります。二重線はstochasticではなくdeterministicに決まる関係を表します。

以下の吹き出しの順に説明していきます。

①

ハイパーパラメータ, からgamma分布に従ってK次元vectorがM個作られます。これを横に並べてM×Kの行列にします。

②

はNB, UM, LDAと同様です。V次元simplexがK個作られます。これを横に並べてK×Vの行列にします。

③

ここでは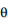とを掛けることでM×Vの行列evを作成します。

④

行列evの各成分をパラメータとしてpoisson分布から単語の出現回数を生成します（bag-of-wordsである行列Wの成分を生成します）。

Stanの実装は以下になります。

data {
   int<lower=1> K;               # num topics
   int<lower=1> M;               # num docs
   int<lower=1> V;               # num words
   int<lower=0> W[M,V];          # bag of words
   vector<lower=0>[K] Alpha1;    # topic prior1
   vector<lower=0>[K] Alpha2;    # topic prior2
   vector<lower=0>[V] Beta;      # word prior
}
parameters {
   matrix<lower=0>[M,K] theta;   # component score matrix
   simplex[V] phi[K];            # word dist for topic k
}
transformed parameters {
   matrix[K,V] clm;              # component loading matrix
   matrix[M,V] evm;              # expected value matrix
   for(k in 1:K)
      for(v in 1:V)
         clm[k,v] <- phi[k,v];
   evm <- theta * clm;
}
model {
   # prior
   for (m in 1:M)
      theta[m] ~ gamma(Alpha1, Alpha2);
   for (k in 1:K)
      phi[k] ~ dirichlet(Beta);

   # likelihood
   for (m in 1:M)
      for (v in 1:V)
         W[m,v] ~ poisson(evm[m,v]);
}

17-19行目ではsimplexではそのまま行列として扱えないので繰り返しで単純にコピーしています。結局StanではデータからM×Kの行列thetaとV面サイコロphi（K個）を推定することになります。パラメータの総数はLDAと変わりません。フルベイズの場合はgamma分布を使っている分だけLDAより少しパラメータ数が増えます。

これをキックするRのコードは以下になります。

library(rstan)

load("input/201402_data1.RData")

data <- list(
   K=K,
   M=M,
   V=V,
   W=bow,
   Alpha1=rep(1, K),
   Alpha2=rep(1, K),
   Beta=rep(0.5, V)
)

fit <- stan(
   file='model/GaP.stan',
   data=data,
   pars=c('theta', 'phi'),
   iter=1000,
   chains=1,
   thin=1
)

• 9行目: データとしてbag-of-wordsを渡すことに注意。
• 10-11行目: gammma分布のハイパーパラメータを与えています。rep(0.1,K)などのより無情報なパラメータを使ってもよいと思いますし、データが多ければフルベイズで求めたいところです。
• 18行目: stan関数の引数にpars=c('パラメータ名')を与えることで、そのパラメータ名だけ値の保存をします。これがないと大きな行列の推定値も保存してしまいます。

結果は以下になります。 LDAの時と同様、1文書あたりの総単語数が少ない場合（data1; 20単語程度）は収束しましたがトピックが分離できていませんでした。1文書あたりの総単語数が多い場合（data2; 150単語程度）は収束しました。thetaとphiは以下の通り。

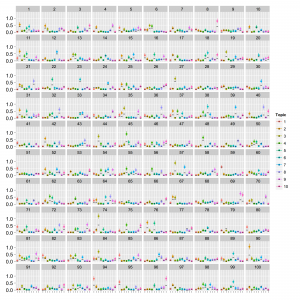
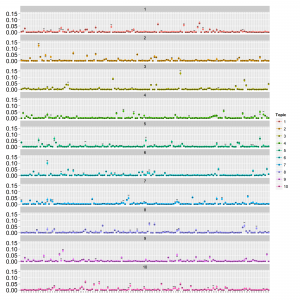
点はMCMCサンプルの中央値で範囲は80%信頼区間です。thetaは横軸:トピックのインデックス、縦軸:確率で、文書ごとにプロットしています。phiは横軸:単語のインデックス、縦軸:確率でトピックごとにプロットしています。真の値を黒の横棒で表しています。thetaは直接比較はできませんが参考のため推定値を50で割ってから真の値と重ねてplotしています。かなりうまくいっているように見えます。[Buntine+ 2005]をもとに実装して、たぶんあってると思いますがもし誤りありましたら教えてください。

最後にモデルのパラメータ数（Stanで出力される数です。ホントはsimplexの制限があるので実質的な数は少し減ります）や推定にかかった計算時間などは以下の通りです。

項目	文書あたりの単語数	NB	UM	LDA	LDA(Freq)	PAM	GaP
パラメータ数	少/多	1450	1450	2440	2440	4740	2440
計算時間	少	5.5m	2.3m	7.7m	7.4m	16.6m	10.9m
収束具合	少	○	×	○	○	○	○
lp__	少	-13892	-13882	-16920	-16919	-23091	-11746
計算時間	多	30.8m	11.7m	53.7m	30.4m	69.9m	12.2m
収束具合	多	○	○	○	○	△	○
lp__	多	-74154	-75760	-76793	-76787	-83274	-22534