StanとRでレプリカ交換MCMC(parallel tempering) を実行する
本記事は発展的な話題です。かつて@Med_KUさんのブログ記事「てさぐれ!!RStanもの」で出てきた例題は局所最適値(local minimum)が多くて、Stanで実行する際も初期値をかなりピシッと決めておかないとダメな例題でした。
しかし、モデルが高次元になってくると最初から“それらしい”初期値なんて分かりようがないし、そもそも理論的にはどんな初期値からはじめても長い間iterationをとれば大域最適値に到達してほしいです。しかし、Stanとは言え、現実的な時間内では局所最適値につかまります。溝が少し深いと出てこれません。そんな状況を打破するための発展的なMCMCの手法の1つに「レプリカ交換MCMC(replica exchange MCMC)」というものがあります。パラレルテンパリング(parallel tempering)としても知られています。
例によってここでは詳しく説明しません。以下の書籍を参考にしました。
この本のp.74-78 この本のp.60-66Web上で閲覧できる情報としては以下がおすすめです。
- [1] 統計数理研究所の伊庭先生による「参考書 モンテカルロ法入門 - 統計数理研究所」 (pdf file)
- [2] レプリカ交換MCMC講義 (伊庭幸人) 難易度 - YouTube (Web link)
- [3] Y. Iba, "Extended Ensemble Monte Carlo," Int. J. Mod. Phys. C, 12, pp.623-652, 2001.(arXiv)
Stanはコンパイルしたオブジェクトを使いまわすことができるので、BUGSと違ってレプリカ交換法が大変やりやすいです。またAWSなどを使えばレプリカの数だけ並列化も簡単にできますので、モデルが高次元で収束が遅い時や局所最適値につかまりやすい時の必殺技として期待しています。「MCMCで初期値をセットするのは負けた気がする」とはおさらばできそうです。
それでは今回は先ほど取り上げた例題に対してレプリカ交換法を行ってみます。都合によりデータを生成する際の乱数の種を固定し、X=0の点は除き、変数の名前を少し変えました。まずはデータの作り方は以下です。
グラフは以下です。
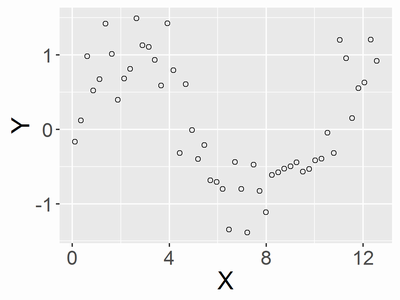
Stanコードは以下になります。
- 5行目: 逆温度です。外からデータとして渡します。逆温度が1の時が元のモデルと一致します。
- 14行目:
Eはエネルギーです。低くなればなるほどいい量なので引きこんで作っていくことに注意。 - 17~18行目: 事前分布の
Eへの寄与です。弱情報事前分布を使っています。なくてもOKですが、bが120ぐらいの値もとてもEが低くなるのでそういうことを防ぐために設定しています。単なる例題ですのでいろいろ変えてみてもよいでしょう。 - 27行目: 対数事後確率としては定数項を無視して
-InvT * Eになるので、それをStanに伝えています。
Stanは対数事後確率がより大きなところからより多くサンプリングします。符号が逆のEから見ると、より低いところからより多くサンプリングします。このモデルのE(エネルギー)の等高線を見ておきましょう。
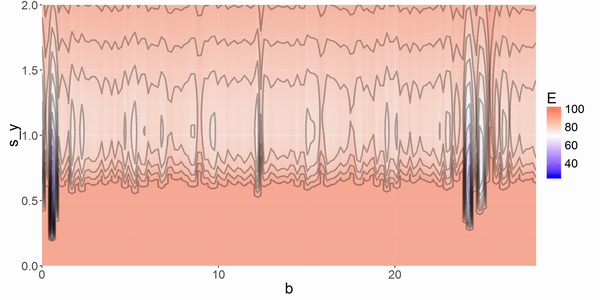
恐るべき局所最適の多さ。bが[0, 1.5]と[23.5, 24.5]を拡大したものは以下の通りです。
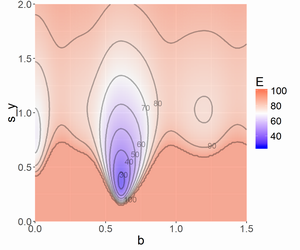
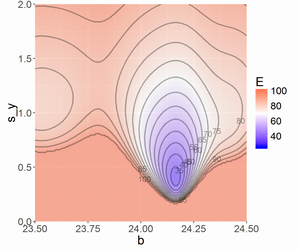
わずかにbが小さい方がEが小さいようです。今はbとs_yの2つしかないのでEの等高線が描けてなんとなくどんな状況か分かりましたが、パラメータの数が少しでも増えると等高線を描くことはできません。
このモデル(逆温度が1の時)で何も考えずにstanを実行するとどんな感じのtraceplotになるかを表したのが以下の図です。

もろ局所最適値にひっかかっており、iterationをこのまま伸ばしても最もEが低いところにはなかなか到達できません。そこでレプリカ交換法の出番です。温度が高いところ(逆温度の低いところ)では、Eの等高線はほとんど無視できるほどパラメータが自由に動けます。そこで温度が異なる実行系列(レプリカ)をたくさん用意して、時々レプリカ間でパラメータの値を交換します。すると、局所最適に一度はまったとしても温度が高いところを経由して抜け出すことができるようになるイメージです。
レプリカ交換法のRコードは以下になります。
- 4~51行目: 関数の定義です。後から説明します。
- 56行目: 初期値は意地悪して、嬉しくない方のかなり深い局所最適値の所にしました。果たして脱出することができるのか。
- 57行目: Stanファイルのコンパイルだけ行っています。
- 60行目: レプリカの数を定義します。
- 61行目: 交換タイムの回数を定義します。
- 62行目: 逆温度を0.02~1までの等比数列で10個になるようにしているだけです。
64行目:
{doParallel}パッケージを使って並列化しています。コア数は3にしていますがレプリカの数だけとりたいです。65~66行目: レプリカ交換MCMCを行う関数には、各レプリカの逆温度・交換タイムの回数・モデルとデータ・
parameterブロック内のパラメータの名前と次元を伝えるリスト・初期値・短いサンプリングのiterとwarmupの回数を指定します。par_listについて補足しますと、例えばparameterブロック内のパラメータがvector[3] theta[5]だけならpar_list=list(theta=c(5,3))になります。- 7行目:
par_listを使うとすべてのパラメータの個数をこのように求めることができます。 - 8行目: T=1 におけるMCMCサンプルを格納します。
- 9行目: 交換をするためのレプリカの番号を格納しておくテーブルです。
- 10行目: その時の
E(エネルギー)ものちの図のため記録しておきます。 - 13行目: はじめの交換タイムの時に、レプリカの番号1⇔2, 3⇔4, ..., 9⇔10 の交換を試します。次の交換タイムの時には2⇔3, 4⇔5, ..., 8⇔9 の交換を試します。これらを交互に試します。そのための添え字づくりをしています。この方法は書籍を参考にしました。レプリカが少ないときは並列化しなくても十分速いので並列化していません。
- 16~22行目: 各レプリカで独立に並列でサンプリングしています。17行目で逆温度を、19行目で初期値を設定しています。
- 23行目: T=1のレプリカのMCMCサンプルを格納しています。
permuted=FALSEはMCMCのサンプル系列の順番を保存する意味で、inc_warmup=FALSEはwarmupを除いた期間のみを格納する意味です。Stanではwarmup期間はパラメータのadaptationの期間ですので、今回は取り除きました。 - 26~36行目: レプリカの交換を確率的に行っています。26行目で各レプリカの
Eの最後のMCMCサンプルを取り出しています。29行目でレプリカ間の交換確率wを算出しています。30~33行目で一様乱数rより大きいときに交換が実施され、交換テーブルに記録されます。 - 39~47行目: 交換テーブルに従って、各レプリカにおけるパラメータの最後のMCMCサンプルをとってきて、初期値にセットしています。ここで任意のモデルで実行できるようにするために
par_listが必要になりました。
計算時間はSurface Pro 3(core i5)で2分ぐらいでした。普通にStanを実行するのと比べるとかなり遅く感じますが、今回のモデルの場合は各Stanのiter=70の実行が0.5秒以下であり並列化のメリットがあまりなく、交換タイムを待つ方が律速になっていること、使っているコア数 < レプリカの数であることが原因だと思います。もっと複雑なモデルでは、Stanのiter=70の実行が10秒以上かかるようになりますので並列化の効果が出ると思います。そのうちやってみます。
結果は以下になります。
まずは交換の様子とEの挙動(全レプリカが見れるようにしたものと縦軸を100までにしぼったもの)から。
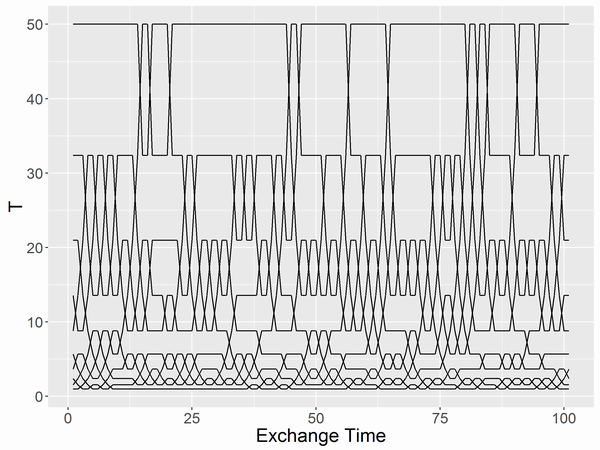
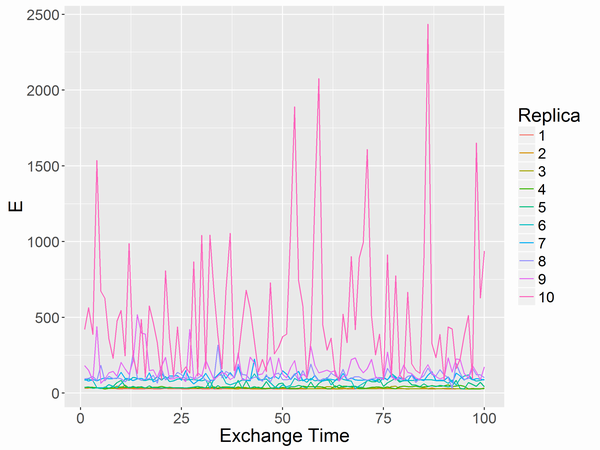
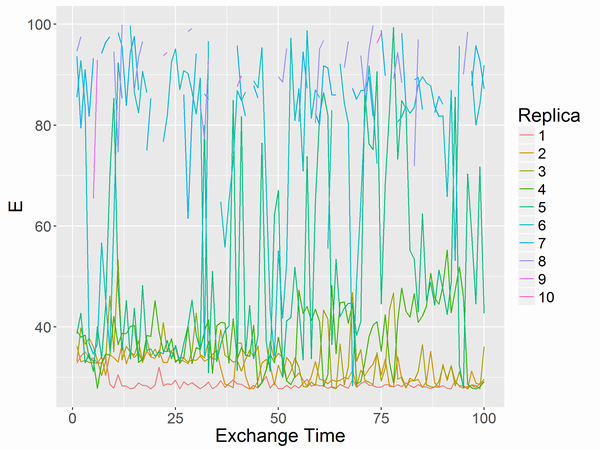
交換の様子と見ると、レプリカの間で交換がなさすぎるや交換が多すぎるところがあると問題ですが、そんなこともなくうまくいってそうです。交換の回数は30%超えないぐらいがよいと教えてもらいましたがそれより少し多そうです。Eの方を見ると交換タイム10を過ぎたあたりから局所最適値を抜け出して、よりEの低いところへ行けたことが分かります。これらの図を描くコードは記事の最後にあります。
得られたms_T1からtrace plotを描いたものが以下です。
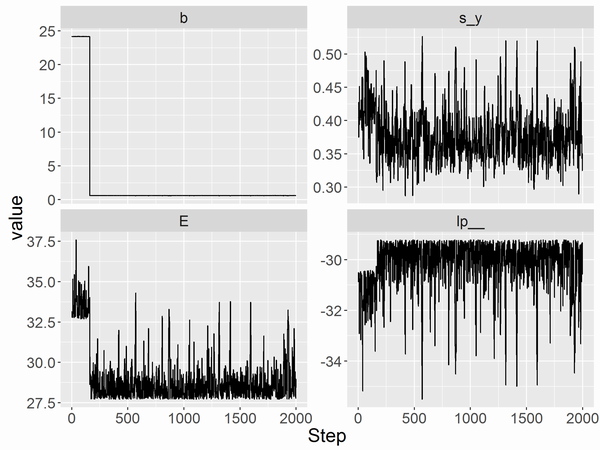
感想としましては、レプリカの数と逆温度を決める部分がモデルに依存するのが実務的に少し難しいところです。僕ははじめに少ない交換タイム回数で試し打ちを何回かやってから決めました。書籍によりますと適応的にレプリカを作る方法もあるようです。論文をまだ読んではいませんが、交換があまりないところにレプリカを作っていく感じでしょうか。もう少し使ってみて経験を得ようと思います。Tokyo.StanのBetancourt氏の講演ではそういったレプリカを用意する必要のない「Adiabatic Monte Carlo」(arXiv)を教えてもらいました。アニメーションが超かっこよかったのであとで読んでみたいと思います。
交換の図やEの図を描いたRコード
2016.6.4にこの内容で発表しました。

