import pandas as pd
from pystan import StanModel
import matplotlib.pyplot as plt
import pickle

d = pd.read_csv('input/data-attendance-1.txt')
d.Score /= 200
data = d.to_dict('list')
data.update({'N':len(d)})

stanmodel = StanModel(file='model/model5-3.stan')

# NUTS (No U-Turn Sampler)
fit_nuts = stanmodel.sampling(data=data, n_jobs=1)
mcmc_sample = fit_nuts.extract()
mu_est = mcmc_sample['mu']

# ADVI (Automatic Differentiation Variational Inference)
fit_vb = stanmodel.vb(data=data)
vb_sample = pd.read_csv(fit_vb['args']['sample_file'].decode('utf-8'), comment='#')
vb_sample = vb_sample.drop([0,1])
mu_est = vb_sample.filter(regex='mu\.\d+')

with open('output/model_and_result.pkl', 'wb') as f:
    pickle.dump(stanmodel, f)
    pickle.dump(fit_nuts, f)

6～9行目：　データを読み込んでpandasのDataFrameを作り、そこからStanに渡せるようにdictionaryに変換しています。7行目ではデータのScoreをスケーリングしています。推定したいパラメータのスケールを同じぐらいに揃えるのが目的です（収束が改善する場合があります）。
11行目：　Stanファイルのコンパイルだけを行っています。初期値を変えたりiterを変えたりしてサンプリングをいろいろ試したい場合に便利です。
14行目：　NUTSというアルゴリズムでサンプリングを実行しています。デフォルトだとコア数の分だけ並列で実行されます。しかし、Windowsの場合は無限コンパイル地獄に落ちる不具合があるので、n_jobs=1で並列を止める必要があります。このページを参照。
15～16行目：結果からMCMCサンプルを入手する一例です。
19～22行目：　NUTSではなく、自動変分ベイズ（ADVI）で推定する場合です。結果の形式がまだ洗練されておらず、ファイルから読み込んでからゴミの行を除去する必要があります（簡単ですが）。
24～26行目：　コンパイルされたモデルと結果をpickleで保存しておきます。

実行速度は基本的にC++コンパイラに依存するだけなので、Rの場合（少し古いgcc）と大きな差はなさそうです。

収束の要約とtraceplotの保存

本の4.4.8項「収束診断をファイルへ出力する」に相当します。pystanのデフォルトのプロット関数を使ってfit_nuts.plot()のようにするとtraceplotを描くことができますが、4つのchainを線種を変えて描くのではなくて1つのchainにまとめて描いてしまったり、表示がつぶれたりする不満点があります。代わりの関数としては、PyMCの開発チームが作成中のmcmcplotlibに期待していますが、例も使い方も載ってないので躊躇してしまいます。ここでは自作でRの{coda}パッケージ風のtraceplotを、複数ページのpdfで作成することにしました。

import pickle
import sys
import numpy as np
import math
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.backends.backend_pdf import PdfPages

with open('output/model_and_result.pkl', 'rb') as f:
    stanmodel = pickle.load(f)
    fit_nuts = pickle.load(f)

## summary
with open('output/fit-summary.txt', 'w') as f:
    f.write(str(fit_nuts))

## traceplot
palette = sns.color_palette()
ms = fit_nuts.extract(permuted=False, inc_warmup=True)
iter_from = fit_nuts.sim['warmup']
iter_range = np.arange(iter_from, ms.shape[0])
paraname = fit_nuts.sim['fnames_oi']
num_pages = math.ceil(len(paraname)/4)

with PdfPages('output/fit-traceplot.pdf') as pdf:
    for pg in range(num_pages):
        plt.figure()
        for pos in range(4):
            pi = pg*4 + pos
            if pi >= len(paraname): break
            plt.subplot(4, 2, 2*pos+1)
            plt.tight_layout()
            [plt.plot(iter_range + 1, ms[iter_range,ci,pi], color=palette[ci]) for ci in range(ms.shape[1])]
            plt.title(paraname[pi])
            plt.subplot(4, 2, 2*(pos+1))
            plt.tight_layout()
            [sns.kdeplot(ms[iter_range,ci,pi], color=palette[ci]) for ci in range(ms.shape[1])]
            plt.title(paraname[pi])
        pdf.savefig()
        plt.close()

9～11行目：　pickleで保存した結果を読み込んでいます。
14～15行目：　MCMCサンプルの要約（Rhatなどの収束診断を含む）をファイルに出力しています。
18～40行目：　traceplotを描いています。
- 18行目： chainごとの色をseabornパッケージのデフォルトカラーパレットで決めています。このままですとchainの数が6を超えたらエラーが出ます（色が巡回するようにすればOKと思います）。
- 19行目：　extract関数はMCMCサンプルを取り出す関数ですが、デフォルトだと各chainを混ぜて、iterationの順番も混ぜて出力します。開発チームの想定と異なる使われ方を防ぐためだそうです（ここ参照）。traceplotをプロットするにはchainごとにiterationの順番を保持したままのMCMCサンプルが欲しいので、このように引数を指定しています。
- 20～21行目：　ここではRの{rstan}パッケージと同様に、warmup期間を除いた部分のtraceplotと密度関数を描くようにしました。もしwarmup期間も含めてプロットしたい場合にはiter_from = 0としてください。
- 22～23行目：　複数ページのpdfを作るためにパラメータ数を取得しています。1ページに4つのパラメータを描きます。
- 25～40行目：　残りはmatplotlibの話なのでここでは省略します。複数ページのpdfの作成方法は公式ページを参考にしました。

結果の図は以下になります（pdfの1ページ目です）。

f:id:StatModeling:20201106182522p:plain

実測値と予測値のプロット

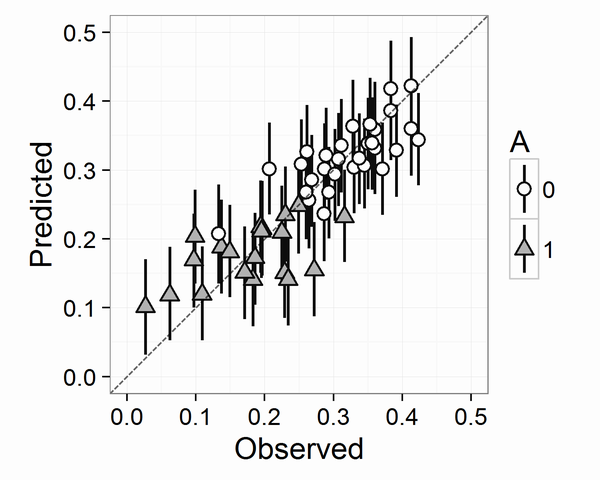
本の5.1.8項「図によるモデルのチェック」に相当します。図5.3を描きます。横軸に実測値（データ）・縦軸に予測分布の中央値と予測区間をプロットしたグラフです。

このようなグラフを描くにはMCMCサンプルを集計したり加工したりする必要があります。岩波DS1のGitHub リポジトリ内に、sinhrksさん（pandasのコミッタ）に書いてもらったコードがありますので、よくそれらを参考にしています（example1,example2,example3）。

Pythonコードは以下になりました。

import pickle
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

with open('output/model_and_result.pkl', 'rb') as f:
    stanmodel = pickle.load(f)
    fit_nuts = pickle.load(f)

d_ori = pd.read_csv('input/data-attendance-1.txt')
ms = fit_nuts.extract()

quantile = [10, 50, 90]
colname = ['p' + str(x) for x in quantile]
d_qua = pd.DataFrame(np.percentile(ms['y_pred'], q=quantile, axis=0).T, columns=colname)
d = pd.concat([d_ori, d_qua], axis=1)
d0 = d[d.A == 0]
d1 = d[d.A == 1]

palette = sns.color_palette()
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot([0,0.5], [0,0.5], 'k--', alpha=0.7)
ax.errorbar(d0.Y, d0.p50, yerr=[d0.p50 - d0.p10, d0.p90 - d0.p50],
    fmt='o', ecolor='gray', ms=10, mfc=palette[0], alpha=0.8, marker='o')
ax.errorbar(d1.Y, d1.p50, yerr=[d1.p50 - d1.p10, d1.p90 - d1.p50],
    fmt='o', ecolor='gray', ms=10, mfc=palette[1], alpha=0.8, marker='^')
ax.set_aspect('equal')
ax.set_xlim(0, 0.5)
ax.set_ylim(0, 0.5)
ax.set_xlabel('Observed')
ax.set_ylabel('Predicted')
fig.savefig('output/fig5-3.png')

14～19行目：　MCMCサンプルの分位点（ここでは10%点, 50%点, 90%点）を計算してDataFrameにしています。行や列をしぼるのがラクで、描くときに便利だからです。

残りはmatplotlibの話なのでここでは省略します。結果の図は以下になります。

f:id:StatModeling:20201106182514p:plain

MCMCサンプルの散布図行列

同じく本の5.1.8項「図によるモデルのチェック」の、図5.5に相当する図を描きます。Pythonで散布図行列を描くにはseabornパッケージのPairGridを使うのが便利です。ただし、上三角行列の部分はカスタマイズする必要があります。ここを参考にしました。

import pickle
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
from matplotlib.patches import Ellipse
from scipy import stats

with open('output/model_and_result.pkl', 'rb') as f:
    stanmodel = pickle.load(f)
    fit_nuts = pickle.load(f)

d_ori = pd.read_csv('input/data-attendance-1.txt')
ms = fit_nuts.extract()

def corrfunc(x, y, **kws):
    r, _ = stats.spearmanr(x, y)
    ax = plt.gca()
    ax.axis('off')
    ellcolor = plt.cm.RdBu(0.5*(r+1))
    txtcolor = 'black' if math.fabs(r) < 0.5 else 'white'
    ax.add_artist(Ellipse(xy=[.5, .5], width=math.sqrt(1+r), height=math.sqrt(1-r), angle=45,
        facecolor=ellcolor, edgecolor='none', transform=ax.transAxes))
    ax.text(.5, .5, '{:.0f}'.format(r*100), color=txtcolor, fontsize=28,
        horizontalalignment='center', verticalalignment='center', transform=ax.transAxes)

d = pd.DataFrame({'b1':ms['b1'], 'b2':ms['b2'], 'b3':ms['b3'], 'sigma':ms['sigma'],
                  'mu1':ms['mu'][:,0], 'mu50':ms['mu'][:,49], 'lp__':ms['lp__']},
                  columns=['b1', 'b2', 'b3', 'sigma', 'mu1', 'mu50', 'lp__'])
sns.set(font_scale=2)
g = sns.PairGrid(d)
g = g.map_lower(sns.kdeplot, cmap='Blues_d')
g = g.map_diag(sns.distplot, kde=False)
g = g.map_upper(corrfunc)
g.fig.subplots_adjust(wspace=0.05, hspace=0.05)
for ax in g.axes.flatten():
    for t in ax.get_xticklabels():
        _ = t.set(rotation=40)
g.savefig('output/fig5-5.png')

17～26行目：上三角行列を作成しています。Spearmanの順位相関係数に応じて、楕円の太さ細さと色を変えています。数値は相関係数×100を表示しています。
36行目： subplotの間の空白を狭くしています。空いていると少し見づらかったので。
37～39行目： X軸ラベルを少し傾けています。PairGridなので少しややこしいです。

結果の図は以下になります。

f:id:StatModeling:20201106182518p:plain

まとめ

pystanを使ってPythonからStanを実行してみました。思ったより簡単です。
numpyやpandasはMCMCサンプルと相性がよくて楽しいです。
作図の部分はRを使う場合と同様で、自分である程度頑張る必要があります。matplotlib力が試されます。
「StanとRでベイズ統計モデリング」をPythonで実行するのは十分可能と思いました。

2016-10-02

ゲルマン先生の「役に立つ統計用語集」

理論

この記事はゲルマン先生（Andrew Gelman）の許諾を得て、Handy statistical lexiconを日本語訳したものです。元記事の用語集は現在も更新中です。英語に抵抗がない人はぜひ元記事を読んで下さい。訳語に関しては親しみやすさを重視し、多くの日本人にあまりなじみのないと思われる言葉や地名は変え、難しい熟語は避けました。また、訳注はリンク先の要約をしばしば含みます。

ここで取り上げるものはすべて重要な手法や概念である。それらは統計学に関連しており、よく知っておくべきにもかかわらずあまり知られていないものだ。それらに名前を与えることで、そのアイデアがもっと親しみやすいものになってほしいと思う。

ミスターP: マルチレベル（階層モデル）で回帰し、事後層別化（poststratification）する手法のこと。
秘密兵器: ある統計モデルを複数の異なるデータセットに繰り返しあてはめて、すべての推定値を同時に表示すること。
スーパープロット: 交互作用があるモデルの推定値をプロットした折れ線グラフの一種。グループごとにあてはめた回帰直線を引く。また、その直線上の（X, Y）に点をプロットする。点の大きさ（面積）は、あるグループ内でXの値を持つサブグループの大きさを表す。
まず自分を疑え: 計算がうまくいかないとき、しばしばあなたのモデルに問題がある。*1
代打が優秀な打者とは限らない: ただ一つのことを仕事にしている人は、その一つのことも常に得意とは限らない。
- 訳注:　同僚は著作の誤植を多数指摘してくれるにもかかわらず、編集者は見落としがひどいというゲルマン先生の経験から。
弱情報事前分布: 無情報事前分布を使いたいと思ったときに使うべきもの。
- 訳注:　StanのWikiにオススメの弱情報事前分布がある。
P値とU値: 両者は違うもの。
- 訳注:　ゲルマン先生の2003年の論文の中にU値について説明がある。伝統的な統計学ではデータを確率変数とみなし、P値は一様分布（Uniform）に従う。それはU値と呼ぶべきものだと主張している。一方でベイズ統計ではパラメータを確率変数とみなし、P値は事後確率から算出した何らかの確率となる。
保守主義: 統計学においては、以前に使われたことがある手法を使いたいという欲望。
ジェニファーならどうする？: 応用統計学の問題で行き詰まったときに考えてみること。*2
- 訳注:　ジェニファー（Jennifer）はゲルマン先生と共著で通称ARMを書いた人。
理論統計学者と応用統計学者の見分け方: 理論統計学者はデータにxを使い、応用統計学者はyを使う（xは説明変数のためにとっておく）。
「片方にしか賭けない」の誤り: パスカルの賭け、宝くじなどなど。
- 訳注（リンク先の要約）:　生徒に「10億分の1の確率で負けて死ぬ賭けがあって、勝った場合にいくらもらえるならその賭けをやるか」と質問したところ、誰もやりたがらなかった。しかし、100円ケチって道路を横切るのと大して変わらない。宝くじも当たる方だけに気をとられず、毎回3000円以上購入して外し続けた場合も考えよ。つまり、このような「片方にしか賭けない」の誤りのポイントは、人々は問題の半分側しか見てないことと、トレードオフがあることを全く認識していないことだ。
何でもアルファベット順にするな: アメリカの統計学者Howard Wainerの言葉で「Alabama First」という言葉がある。もっとよい並べ方があるにもかかわらず、アルファベット順に並べて図を描くという失敗に対する言葉。
- 訳注:　アメリカの州一覧をアルファベット順にするとAlabamaが先頭にくることから。*3
47NEWS（よんななニュース）の誤り:　すべての県（や国）を等しく扱ったり、より管轄の大きな場所により多くの人が住んでいることを忘れたりしてはいけない。もし、面積が同じくらいとはいえ神奈川県を佐賀県と同じように扱うと、神奈川県の何百万人の人たちを無視することになる。
- 訳注:　日本版に置き換えた。47NEWSは47都道府県の各々のニュースをなるべく同等に扱うことから。*4
二次の可用性バイアス: あなたが個人的に経験した相関を、集団における相関に一般化してしまうこと。
「他は全て等しいとする」の誤り: 他は全て一定になっていなさそうな場合ですら、そう仮定してしまうこと。
自動掃除機能つきエアコン: よいパッケージは自分自身のテストを含んでいるべき。*5
混乱の分類: 行き詰ったときにやるべきこと。リンク先に例がある。統計の授業でTAに尋ねる前に以下のように分類せよ、とのこと。
1. 統計に関する質問。しかし授業の前提知識に入っている場合: 統計の入門書を読め、TAに聞くな。
2. 統計に関する質問。授業の一部に関係ある場合: 本を読め、友達に聞け、それからTAに聞け。
3. 統計的には分かっているが、関数の名前が分からない場合: 「R standard deviation」みたいにググれ。もしくは自分で関数を書け。見つけられなかったら友達に聞け、それからTAに聞け。
4. 関数の名前は分かっているが、どうやって使うか分からない場合: help(sd)のようにタイプしてヘルプを見よ、それから友達に聞け、それからTAに聞け。
5. コードを書いたけどエラーが出る場合: デバッグせよ。printで画面に表示したり、コードをより小さなステップに分けたりせよ。
6. コードを書いてエラーも出ないが、思っていたのと異なる挙動の場合: デバッグせよ。
次元の祝い: より多くのデータがあることは良いこと。たとえその追加された情報が、「データ点」というより「次元（訳注:説明変数や特徴量のこと）」だとしても。
scaffolding: 関連するモデルと比較することで自分のモデルを理解すること。
- 訳注:　scaffoldingは「足場」。ほぼ同じ意味でRuby on RailsなどのWebフレームワークでも使われる。統計モデルにも「足場」があるという主張。
オッカム信者: 他人に過度に単純化されたモデルを使わせようとする癖や傾向のこと。イライラする。
- 訳注:　オッカムの剃刀のオッカム。
ベイジアン: たとえそれが不適切でも、すべての問題に対してベイズ推定を使う統計学者のこと。私自身（訳注:ゲルマン先生）はベイジアンです。
多重比較: もし適切に解析を実行しているなら、一般的に大した問題ではない。しかし、もし手を抜いて階層的な構造を階層的にモデリングしないと大きな問題になりうる。
モデルをあまりに真剣に受け止めるな: モデルをあまりに真剣に受け止めるのは、モデルを全く真剣に受け止めないのとまさに同じ。
- 訳注:　リンク先には「モデルの奴隷になるな、モデルと協力せよ」とコメントがある。
神はあらゆる木のあらゆる葉に宿る: もし本当にすごいことをやろうと思うならば、小さな問題や自明な問題なんてありはしない。
- 訳注:　この説明の文章は物理学者ファインマンの引用
リズムと意味はトレードオフ: 不必要な挿入語句を取るとデコボコになる。*6
- 訳注（リンク先の要約）:　人が理解しやすいように文章のリズムを重視すると、どうしても不必要な挿入語句を加える必要がある。
お話の時間: 数値がベッドに入ったら、お話が出てくる。
- 訳注（リンク先の要約）:　数値を用いた解析結果の説明は客観性や信頼性があるが、結果を踏まえた数値のない「お話」は信頼性が全くないことから。研究者は誰も持ってないような仮説を出すのが仕事なので、特に信頼性がない。
苦しい時のベイズ頼み: 大きくて現実のタフな問題を扱う場合に、何らかの信頼性の問題で私（＝ゲルマン先生）に意義を唱える人はない。*7
ピノキオの原則: 計算上の理由だけで作られたモデルでも独り歩きする可能性がある。
type M error: もし推定値が統計的に有意ならば、それはきっと効果の大きさ（magnitude of effects）を過大評価している。
- 訳注:　リンク先では、統計的に有意なことを優先して効果の大きさを過大評価するエラーを、type I/II errorになぞらえてtype M error　(magnitude)と呼んでいる。
アローのもう一つの定理（弱形式）: どんな研究成果でも最大で5回までしか論文にできない。
アローのもう一つの定理（強形式）: あらゆる研究成果は5回まで論文にできる。
ラマヌジャンの原則:　表は粗いグラフだと思って読め。
- 訳注:　リンク先には表の数値の符号や桁数などをざっと見る話などがある。
哲学のパラドックス: もし哲学を追放すると、ならず者だけが哲学をする。*8
- 訳注:　内容の一貫性のため、ゲルマン先生は著作のBDAやARMから哲学の章を省いた。その結果、ならず者がベイズの哲学を語り、ミシガン大の経済学者が混乱した経験から。
統計学はデフォルトの科学: （リンク先の要約）統計学の他の工学との違いとして、デフォルトの手順に対して特別愛着を持っていることが挙げられる。デフォルトには推定値や本やセッティングなどが含まれ、最近ではデフォルトの事前分布に注力している。デフォルトを選んでおきなさい。
- 訳注:　StanのWikiにオススメの弱情報事前分布がある。
手法のおかげ問題: 素晴らしい統計コンサルタントや共同研究者の多くの有用な貢献は、彼ら/彼女らが使った手法や哲学のおかげだと過度に思われることが多い。
- 訳注:　実際には彼ら/彼女ら自身の創造性が素晴らしい。リンク先にはルービンとエフロンとパールの話がある。
目的が違えば見方も違う: グラフの中にはすでに知っていることを愉快に可視化してくれるものがある。あまりに面白く示されているので、すでに知っていることを再学習する喜びがある。また、新しい視点でグラフを眺め、いろいろな関連トピックについてより深く考えさせられることに気づいて衝撃を受ける。*9
- 訳注:　リンク先ではパッと見ではよくないInfovisの例があるが、そのグラフからも「通話のデータをたくさん持っている人が存在すること」などが分かる、とのこと。
新入生の質問: 新入生がした質問というだけで、それが的外れの質問とは限らない。
富士の樹海: 「なんかいいことないか漁り」や「pハッキング」ではなく、たとえ前もって研究の仮説を設定していたとしても、多重比較は問題になりうる。*10
一方通行の誤り: どの方向にも転がる可能性がある変化に対し、一つの可能性だけを考えること。
多元性のジレンマ: 自分の哲学がたくさんある選択肢のなかの一つでしかないことを認識する言葉。そして、（少なくとも取り組んでいる問題に対し）なぜ自分の哲学が他の選択肢よりも好きなのかを説明しつつも、自分のコントロールを超えた多数のことに左右されてこの哲学を大切にするに至ったと認識する言葉。*11
実験というより霊験: 単なる証拠では殺せない仮説のこと。（社会学者Jeremy Freeseの言葉から引用）*12
- 訳注:　統計はネガティブを証明することはできない。訳者が思いついた例は「水素水が効かないという証拠はない」。
統計の化学療法: 主な結果に少し毒を入れて、有意であることが望ましくない結果のp値を0.05より大きくすること。（社会学者Jeremy Freeseの言葉から引用）
何が分からないかを話せ: 聞きたいこと。
- 訳注（リンク先の要約）:　ふつうに「分かっていることを話せ」にすると、「分かっていること」と「分からないこと」の境界を知ることができる。もし「何が分からないかを私に話せ」にすると、「分かっていること」と「分からないこと」の境界だけでなく、「分からないこと」と「『分からないことが分かってない』こと」の境界に関するヒントも得られる。情報が多いのは良いこと。
サラダのトング: 絵を描くのに使うな。(リンク先の要約）p値は粗いデータの要約であり、生データからp値になるときにたくさんの情報を失っている。論文に記載されたp値を使って科学をすることはサラダのトングを使って絵を描こうとするようなもの。
スケールダウン係数: 論文に記載された推定値をどれほどスケールダウンして考えるべきかを決める係数。
- 訳注:　論文の結果は「盛っている」と考えるわけである。リンク先の例ではスケールダウン係数が1/2の場合（「42%」を「21%」と考える）を扱っている。
カンガルー: カンガルーが元気に飛び跳ねているときに、おなかの袋に入っている羽の重さを量るのに体重計を使うな。
- 訳注:　効果量がすごく小さくて測定誤差がとても大きいような研究に対する揶揄。
マッハGoGoGoの原則: 科学的もしくは大衆文化の作品で最も面白いところは、表立った箇所ではなく、吟味されていない想定であることが時々ある。
- 訳注:　ゲルマン先生がマッハGoGoGoのアニメを見たときに一番面白かったところは、背景に日本の工業の光景が見られた、登場キャラの長いドライブのシーンだったという経験から。
不確実区間（Uncertainty Interval）: 信頼区間や信用区間の代わりに不確実区間と呼ぼう。
- 訳注:　リンク先には三つ理由が書いてあって、要約は次の通り。信頼区間は解釈しにくく、ベイズ流に解釈してしまいがちであること。信頼区間と予測区間の区別があいまいであること。信頼区間が大きいと信頼性が低くて、信頼区間が小さいと信頼性が高いというちぐはぐさ。
もし全てのデータを持っていたらどうする？: 統計学者ルービンの一つ目の質問。
一切のデータを入手する前は何をしていた？: 統計学者ルービンの二つ目の質問。
時間反転して考える: 有意差が出て論文になった発見が、後からより大規模できちんとしている確認実験で再現できなかった場合にどう考えるべきか。
- 訳注（リンク先の要約）:　エイミー・カディは「力のポーズ」を取ると元気が出て成功の確率がアップすることを比較的少ないサンプル数で実験をし、有意差が出たとして論文を出版した。TEDでも同じ内容で話している。しかし後から、より大規模できちんとしているRanehillらの実験ではその結果は再現できなかった。カディは有意差あったんだよ！！とブチ切れる。ゲルマン先生は時間反転して考えてみようと提案する。先にRanehillらの実験で効果なしと判断され、あとから小規模できちんとしてないカディの実験で有意差ありと判断されたら、カディの実験を信じますか？と。ノイズの可能性が高いと思いますよね、と。
クラークの法則: 十分に馬鹿げた研究は詐欺と区別がつかない。*13
要は結婚式であって決して結婚ではない: 科学論文の結果について肝に銘じておくこと。
- 訳注（リンク先の要約）:　科学論文において間違って有意差が出て論文になっても、それを訂正するプロセスは機能していない。それは科学論文は発見を促進するものであって、修正を扱うものではないからだ。つまるところ、科学論文の結果は華やかな結婚式であって、（その後の大変な）結婚という営みではないのだ。
査読の問題: レビューしてるのは仲間だということ。
- 訳注:　リンク先では、査読者含めた全体が誤認していたら間違いが長続きするよ、と警告している。

ここに載せるのを忘れた言葉がたくさんあるのは知っている。私の記憶をリフレッシュさせてほしい。

P.S. いや、定義ゲームでStephen Sennと戦えるとは思ってないよ。

*1:元の用語はフォーク定理（The Folk Theorem）。数学の諸分野では、「証明をつけようと思えばつけられると誰もが思っているが、実際には誰一人としてその証明をつけたことがない定理」のことを一般にフォーク定理と呼ぶことがあることから（Wikipedia）。

*2:元の用語はWWJD。英語ではWhat Would Jesus Do?をWWJDと頻繁に略し、さらにもじってJesusの代わりに人名を入れることも多いため。

*3:元の用語はAlabama Firstでしたが、州になじみがない日本人を考えて変更しました。

*4:元の用語は「新聞紙USA Todayの誤謬」。新聞紙USA Todayは50州の各々のニュースを扱うことから。カルフォルニア州をモンタナ州やデラウェア州と同じように扱う例を挙げている。ちなみに人口はカルフォルニア州 >> モンタナ州 = デラウェア州。面積はカルフォルニア州 = モンタナ州 >> デラウェア州である。日本人にはなじみがないので県に置き換えた。

*5:元の用語はThe Self-Cleaning Ovenでしたが、日本にはそのようなオーブンが普及していないので、親しみやすさのため変更しました。

*6:元の用語は「駅馬車ビジネスで人が言ったように」。席から詰め物をとると馬車の乗り心地がガタガタになることから。

*7:There are no atheists in foxholes. ということわざがある。日本でいうところの「苦しいときの神頼み」。

*8:米国右翼のスローガン When guns are outlawed only outlaws will have guns.「銃の所持を禁止すれば、ならず者だけが所有する」から。

*9:元の用語はクリス・ロック効果。アメリカの俳優クリス・ロックの語録の一つ「我々みなが知っていることは真実だ」から。

*10:元の用語は八岐の園（やまたのその。英語ではThe Garden of Forking Paths）。八岐の園はアルゼンチンの小説家ホルヘ・ルイス・ボルヘスの短編のタイトル。日本では「伝奇集」に収録されている。その中に次の一節があり、混沌とした様子をうまく表現している。"I thought of a labyrinth of labyrinths, of one sinuous spreading labyrinth that would encompass the past and the future... I felt myself to be, for an unknown period of time, an abstract perceiver of the world." しかし、日本語としてやや親しみにくい。そこでイメージが似ており覚えやすい「富士の樹海」とした（実際には遊歩道を外れなければ安全な場所ですが）。なお、ゲルマン先生は「pハッキング」という言葉は意図やズルが含まれているのであまり好きでない。代わりに「The Garden of Forking Paths」が好き。

*11:政治学者ロバート・ダールの著作「多元的民主主義のジレンマ ― 自治 vs. 制御」から。

*12:元の用語はMore Vampirical Than Empirical. 直訳すると「実験による検証というよりもヴァンパイアのようだ」。元の用語のように韻を踏むために苦労して変えました。

*13:訳注:クラークは「幼年期の終わり」などで知られるSF作家。クラークの3つの法則というものがあって、特に3番目の「十分に発展したテクノロジーはマジックと区別がつかない」が頻繁にパロディ化されている。

2016-09-23

「StanとRでベイズ統計モデリング」松浦健太郎という本を書きました

Stan 書評

僕が筆者なので、この記事は書評ではなく紹介になります。まずこの本はRのシリーズの一冊にもかかわらずStanという統計モデリングのためのプログラミング言語の方がメインです。このようなわがままを許してくれた、~~ゆるい~~ふところの深い石田先生と共立出版には感謝しかありません。

StanとRでベイズ統計モデリング (Wonderful R)

作者:健太郎, 松浦
発売日: 2016/10/25
メディア: 単行本

目次と概要

共立出版のページを見てください。GitHubのリポジトリもあります。

前提とする知識

「はじめに」の部分で触れていますが、確率と統計の基本的な知識はある方、R（やPython）で簡単なデータ加工や作図が一通りできる方を想定しています。そのため、確率分布なんて聞いたことがない、プログラミングがはじめて、Rがはじめて、という方が読み進めるのは厳しいかもしれません。なお、Rの基本的な関数しか出てこないので、PyStanとmatplotlib（あるいはSeabornなど）でやるわっていうPythonユーザの方にも十分に読む価値があると思います。

Pythonユーザのための追記

この本を読んで習得できるもの

「統計モデリングの考え方」と「Stanの使い方」の二点です。

統計モデリングの考え方

基本的にデータ解析には「正解」がありません。検定の前提条件にせよ、統計モデルにせよ、機械学習のモデルにせよ、すべてのモデルは仮定にすぎないからです。しかし、ルール無用ではありません。得られた結果が有用であるため、統計モデリングにも沿うべき指針や考え方があります。統計モデリングは従来の検定ベースの統計と比べると、得意分野も考え方も大きく異なります。筆者は仕事がら普段は検定も使っていますが、「ある現象を理解したい・知識を獲得したい・予測したい」といったデータ解析の主目的については、検定では満足できない場合が多いです。その場合、統計モデリングがよい選択肢になります。この本では統計モデリングをきちんと習得できるように、考え方や手順といった正解がないものについても大胆に筆者の主張を書きました。

Stanの使い方

最近Stanを取り上げたデータ解析の本は増えてきています。僕が確認している範囲だけでも以下があります（刊行順）。

しかし、これらの多くは重回帰のような簡単な解析を数ページで紹介しているだけだったり、Stanの文法などは付録だったりしました。「Stanをしっかり学びたい。より美しく、より速く動くように書きたい。」という人にとって十分に満足できる本はこれまでなかったと言えます。しかし、本書はこのニーズにほぼ100%応えた、日本語で読めるはじめての本格的なStan解説書です。

このブログとの関係

いくつかの記事については本の後半の例題とオーバーラップがありますが、基本的には書き下ろしです。本では用語の説明や結果の解釈などの基礎から順番に説明しています。このブログは僕のメモを兼ねているのでやや難しい題材やStanコードが多いですが、本ではそんなことありません。

その他の特徴

例題からはじまる

なるべく具体的なイメージをもって分かりやすくなるように、多くの解説は例題データの解析からはじまります。

図が多い

統計モデリングを含むデータ解析は可視化と密接に関係しているので、図をふんだんに載せています。図と作図のRコードもGitHubにほぼすべてありますので、よろしければ見てください。ただし、作図は各自が好きなパッケージを使えばよいと思っているので作図のRコードの解説は割愛しました。すみません。

数式は難しくない

ベイズ統計の本では1ページまるまる難解な式変形という本も少なくないです。しかし、この本はソースコードとその解説が多めですが、数式は少なめです。式変形も理系の大学一二年生なら引っかかることなく追うことができるでしょう。

Stanの最新版に対応していく

書籍は2.11対応ですが現時点の2.15にもほぼ対応しています。今後もバージョンアップしたら、GitHub上でどの記述が古くなったか書きます。またソースコード自体もアップデートする予定です。

他人からの書評や感想 (追記)

献本勢が多いので褒める言葉は話半分でよいと思いますが、他人から見てよかった章の紹介などは参考になると思います。

MikuHatsuneさん：StanとRでベイズ統計モデリング - 驚異のアニヲタ社会復帰の予備
xiangzeさん：stanとRでベイズ統計モデリングをいただきました。 - xiangze's sparse blog
森林総合研究所　伊東さん：『StanとRでベイズ統計モデリング』：Taglibro de H：SSブログ
吉備国際大学　京極さん：https://kyougokumakoto.blogspot.jp/2016/10/stanr.html
SAMさん：書評: StanとRでベイズ統計モデリング - About connecting the dots.
関西学院大学清水さん：「StanとRでベイズ統計モデリング」をいただきました | Sunny side up!
ajhjhafさん：StanとPythonでベイズ統計モデリングその1 - Easy to type

松浦stan本来た．予想通りすごくいい．本当は素晴らしい統計モデリングの本なのにstanに密着しているのでstanが終了したら使えなくなるのが残念なくらい　北川本はFORTRANコード削って再生できたけど，これはちょっと無理かな
— baibai (@ibaibabaibai) 2016年10月21日

『StanとRでベイズ統計モデリング』@berobero11 さんより献本頂きましたー！やったー！
これまでのベイズ統計の本と違って，実践的で，大事なことが平易に書いていて，多様なモデルについて紹介してあります。これは買いです！https://t.co/Dpiumh70kx pic.twitter.com/T5n6Y7cDsp
— Hiroshi Shimizu (@simizu706) 2016年10月21日

松浦さんの著書「StanとRでベイズ統計モデリング」https://t.co/DUTFrk6iwk を送っていただきました．ありがとうございます．「よし，Stan を使おう！」という気にさせられる本ですよ．しかも，たいへん丁寧に作られていて，ですね… pic.twitter.com/13lOnFPhnr
— 久保拓弥 (@KuboBook) 2016年10月24日

『StanとRでベイズ統計モデリング』はここ数年出続けたベイズ本もしくはStan本の間違いなく決定版。一般的な回帰問題からLDAのようなどちらかと言うとMCMCでフルベイズでやる人の多くない話、そしてStanの鬼門である離散パラメータの扱いまで満載で、素晴らしいです
— TJO (@TJO_datasci) 2016年10月27日

この他にも色々コメントいただいております。ありがとうございます。

読書会・勉強会

読書会が開かれることになりました。大変ありがたいです。

https://atnd.org/events/83097

なお、愛称は「アヒル本」になった模様です（表紙のブロックはアヒルなのです）。

各章の紹介

以下では実物を手に取って見ることができない人のために、どんなことが書かれているか簡単に紹介したいと思います。

はじめに

本書のあらすじが載っています。

f:id:StatModeling:20201106183153p:plain

1～3章は理論編です。数式が多いわけではなく用語の確認の意味合いが強いです。4～5章はStanの入門編です。6章以降は発展編です。6・8・11・12章が本流で、モデルのレパートリーを増やす章になっています。対して、7・9・10章はモデルを改善する章となっています。特に発展編では読者はStanの強力さを実感できると思います。

1章統計モデリングとStanの概要

「統計モデリングとは何なのか？目的は？メリットは？」という点について筆者なりの考えを述べました。またStanなどの確率的プログラミング言語を使うメリットを簡潔に説明しています。一部抜粋します。

確率的プログラミング言語とは「様々な確率分布の関数や尤度の計算に特化した関数が豊富に用意されており、確率モデルをデータにあてはめることを主な目的としたプログラミング言語」である。ユーザーはモデルをプログラミングコードで記述し、データを渡すだけでよい。すると確率的プログラミング言語の方でほぼ自動的にパラメータの値を推定してくれる。このようにモデルの記述と難しい推定計算を分離することによって、モデルの可読性が上がり、バグの混入が激減し、解析者はモデルの試行錯誤に専念できるようになる。特に多数のモデルを試行錯誤する状況で確率的プログラミング言語は真価を発揮するのである。

2章ベイズ推定の復習

確率分布や「 $y \sim Poisson(\lambda)$ 」などの基本的な用語や記法の確認からはじまります。そのあとでベイズ統計とMCMCに関する用語を簡潔に説明しました。扱った用語は以下の通りです。

尤度、最尤推定、過学習、事後分布（事後確率）、事前分布（事前確率）、MCMCサンプル、chain、trace plot、warm up、thinning、ベイズ信頼区間（信用区間）、予測分布、ベイズ予測区間、MAP推定値、無情報事前分布。

3章統計モデリングをはじめる前に

まず一般にデータ解析に必要となる前準備について説明しています。そのあとで統計モデリングの手順を筆者なりに以下のように定型化しました。

解析の目的
データの分布の確認
メカニズムの想像
モデル式の記述
Rでシミュレーション
Stanで実装
推定結果の解釈
図によるモデルのチェック

本書の以降の例題はなるべくこの手順に沿って解析をすすめています。もちろん、現実のデータ解析はこの手順に尽きているわけではなく、あくまでも最低限踏むべきステップの目安です。また、事前知識の役割や、誤解の多いモデルの「正しさ」についても少し触れました。

4章 StanとRStanをはじめよう

インストール方法、基本的な文法、targetとlp__を説明した後で、じっくり単回帰の問題を扱います。この章以降ではStanコード・Rコードとそれらの説明という部分が多くなります。推定結果の見方、収束の判断、trace plotの見方、{ggmcmc}パッケージの使い方、MCMC設定の変更、MCMCサンプルの使い方を説明しています。

5章基本的な回帰とモデルのチェック

重回帰・二項ロジスティック回帰・ロジスティック回帰・ポアソン回帰を扱います。また図によるモデルのチェック方法を数通り紹介しています。使用した図をいくつか載せておきます。詳しくは本を読んでください。

f:id:StatModeling:20201106183157p:plain

f:id:StatModeling:20201106183201p:plain

f:id:StatModeling:20201106183206p:plain

6章統計モデリングの視点から確率分布の紹介

確率分布の軽い紹介はどんな本にも載っていて、常々冗長だ退屈だと感じていました。しかし、統計モデリングにおいて個々の確率分布は必要不可欠なパーツです。そこで、従来の本にはないような「統計モデリングの視点から」の部分になるべく注力して16個の確率分布を紹介しました。

7章回帰分析の悩みどころ

交互作用、対数をとるか否か、非線形の関係、打ち切り、外れ値など、ふつうの統計の教科書にはあまり載っていませんが、実際のデータ解析では必ずといっていいほど直面する悩みどころを取り上げました。

8章階層モデル

階層モデルはグループ差や個人差をうまく扱うための一手法です。ゆっくり導入をした後で応用方法になじめるように、複数の階層を持つ場合や、非線形モデルやロジスティック回帰の階層モデルを取り上げました。

9章一歩進んだ文法

Stanをより美しく、より速く動くように必要な一歩進んだ文法を解説しました。Stanで用意されている型（かた）の説明やベクトル化、行列演算、パラメータの制約、欠測値がある場合などを扱っています。

10章収束しない場合の対処法

統計モデリングの最大の難所は、MCMCが収束しないことだと言っても過言ではありません。しかしながら、その対策を系統的に扱った書籍や情報はあまりありません。ここではその対策を大きく4つの節に分けて説明しています。個人的な経験からは、10.1節の識別性の問題（多重共線性を含む）と10.2節の弱情報事前分布で収束しない場合の8割は解決できそうです。

11章離散値をとるパラメータを使う

Stanの最大の弱点は離散値をとるパラメータが直接的に使えないことです。この章では、log_sum_exp関数と周辺化消去（marginalizing out, summing out）で解決する方法を説明します。応用例として、混合正規分布、ゼロ過剰ポアソン分布、Latent Dirichlet Allocationを扱います。変分ベイズ法の一実装であるADVIも使ってみます。

12章時間や空間を扱うモデル

時系列データを解析するにあたり、応用範囲が広く、解釈がしやすく、拡張性が高い「状態空間モデル」を取り上げました。特に日次の売り上げデータのように、時刻が離散的で等間隔なデータの場合に使いやすいモデルです。季節調整項や変化点検出なども扱います。後半では、時間構造と空間構造の等価性を説明し、マルコフ場モデル（CARモデルとほぼ同じもの）を使った例題を扱っています。

インストール

モデルファイル（Stanファイル）の説明

Stanファイルのコンパイルとサンプリング