蟻本シリーズ 2 ランダムウォーク

今回は以下のランダムウォークの問題を考えます。

I×Jの大きさのグリッドがあります。(1,1)からスタートして、1ターンに上下左右4マスのうち移動できる方向にそれぞれ確率p1,p2,p3,p4で移動します。いくつかのマスには石が置いてあり、通行不可能になっています。(I,J)にはじめて辿り着くまでにかかるターン数の期待値を求めなさい。ただし、(1,1)から(I,J)に移動するパスが少なくとも1つは存在すると仮定します。

例：I = 3, J = 10

     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,]    1    0    1    1    1    0    1    1    1     0
[2,]    1    0    1    0    1    0    1    0    1     0
[3,]    1    1    1    0    1    1    1    0    1     1

0が石があるマスで、1が移動できるマスです。以降ではこのグリッドを「グリッドA」と呼びます。

蟻本の4-1節（p.257）では、上下左右へ移動する確率が等確率の場合を扱っています。

プログラミングコンテストチャレンジブック [第2版]　～問題解決のアルゴリズム活用力とコーディングテクニックを鍛える～

この問題は期待値についての連立方程式を立てて解くと速いようです。

ここで、をからスタートした場合にゴールするまでにかかるターン数の期待値とします。ただし、は行方向（上下方向）、は列方向（左右方向）の添え字です。から上下左右に移動可能な場合には、次の関係式が成り立ちます。

なぜなら、の確率でへ移動する場合は期待値はからの期待値に今移動に使った1ターンを加えたもの、の確率でへ移動する場合は期待値はからの期待値に今移動に使った1ターンを加えたもの、…となり、各場合は排他的なので和になるからです。この式を整理すると以下になります。

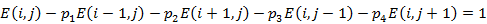
ここで、例えば（左のマスに石があっていけない）の場合を考えます。になった影響で～が正規化されます。すると、同様の考察で以下の式が成り立ちます。

つまり、の場合にも拡張すると、以下の関係式が成り立ちます。

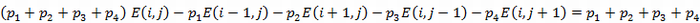
これをすべてのの組み合わせについて行列形式で書き下します。から移動する場合だけを抜き出して書くと以下になります。

_0_は0が続くことを表しています。この式は期待値に関する連立方程式になっています(以下★式と呼びます)。これは行列演算で簡単に解くことができます。

---

以上は自分用の備忘録でした。以下では次のような問題を考えます。

グリッドAがあります。あるロボットが(1,1)からスタートして、1ターンに上下左右4マスのうち移動できる方向にそれぞれ未知の確率p1,p2,p3,p4で移動します。いくつかのマスには石が置いてあり、通行不可能になっています。そして、(I,J)にはじめて辿り着くまでにかかるターン数の期待値を10回測定しました。結果は測定誤差を含めてY <- c(68.8, 75.4, 111.2, 81.4, 82.6, 114.3, 89.2, 54.7, 66.3, 71.1)でした。この結果からp1,p2,p3,p4を推定することを考えます。

Stanでの実装例は以下になりました。

• 2～36行目： 方程式を解いて期待値を返す関数です。
• 3～5行目： Aは★式の左辺の行列、bは★式の右辺のベクトル、resは★式の左辺の期待値のベクトルです。
• 7～10行目：　はじめにゼロで埋めています。
• 14～15行目： ゴール地点と石があるマスの期待値はゼロです。そのため、このようにに掛かる係数を1にしておけば、右辺はゼロ埋めのままなので、となります。
• 17～30行目： Aとbの係数を冒頭の議論をもとに埋めています。
• 34行目： Stanの行列演算を使って方程式を解いています。内部ではC++のEigenの関数が呼ばれています。
• 35行目： res[1,1]が(1,1)から出発した場合のターン数の期待値になります。
• 65行目： 期待値に測定誤差が加わってYになっています。

実行するRコードは以下の通りです。

推定結果は以下になりました。

	mean	se_mean	sd	2.5%	25%	50%	75%	97.5%	n_eff	Rhat
p[1]	0.25	0.00	0.12	0.04	0.15	0.23	0.35	0.48	710	1.00
p[2]	0.26	0.00	0.13	0.05	0.15	0.25	0.36	0.52	921	1.00
p[3]	0.08	0.00	0.05	0.00	0.03	0.07	0.12	0.17	1032	1.00
p[4]	0.42	0.01	0.15	0.20	0.29	0.39	0.52	0.77	743	1.00
sigma	11.79	0.10	3.43	7.15	9.42	11.18	13.42	20.01	1077	1.00
mu	75.95	0.06	3.81	68.34	73.58	75.85	78.36	83.54	4000	1.00
lp__	-33.24	0.05	1.54	-37.11	-34.05	-32.90	-32.10	-31.28	932	1.00

このグリッドAにおいて、上下左右へ移動する確率が等確率の場合には期待値は361.0になります。今回与えた測定データはおよそ平均が80なので、比較するとだいぶ小さい期待値です。そのため、右へ移動してゴールに近づく確率（p[4]）がかなり高く、左へ移動する確率（p[3]）がかなり低く推定されています。

蟻本シリーズ 1 ナップサック問題

「プログラミングコンテストチャレンジブック [第2版]」（通称：蟻本）という本がとてもよかったので、これから3回にわたって統計モデルを絡めた感謝の記事を書こうと思います。

プログラミングコンテストチャレンジブック [第2版]　～問題解決のアルゴリズム活用力とコーディングテクニックを鍛える～

競技プログラミングはたまに実務で役に立たないとか言われていますが、僕はまったくそうは思いませんでした。プログラマーとしてもデータ解析者としても有益な考え方が満載で、ふと気づけば応用できる対象は至る所にあるように思いました。

---

今回は以下のナップサック問題と呼ばれる問題を考えます。

重さと価値がそれぞれWeight[i], Value[i]であるようなN個の品物があります。これらの品物から、重さの総和がMax_Wを超えないように選んだときの、価値の総和の最大値を求めなさい。

蟻本では2-3節（p.52）になります。検索しても解説がいくつか見つかります（例）。

この問題を速く解く方法は漸化式でdp（dynamic programming）テーブルを作る方法です。なんとのオーダーで解けます。ここでは詳しい解説は省略しますが、蟻本から例題を引用してN = 4,(Weight, Value) = {(2, 3), (1, 2), (3, 4), (2, 2)} (i = 1,2,3,4),Max_W = 5の場合について簡単に説明します。

• dp[i, w]を「i番目までの品物から重さの総和がw以下となるように選んだときの価値の総和の最大値」とします。dpは2次元配列でインデックスが0からはじまるとします。この設定がポイントです。
• dp[0, w] = 0 (w = 0, 1, ..., Max_W)になります。なぜならi = 0は「品物なし」の状態で価値の総和は常にゼロだからです。

ここからi = 1の場合、i = 2の場合、・・・のdp[i, w]を以下の漸化式で順番に決めていきます。

• もしw < Weight[i]ならばi番目の品物（重さWeight[i]）を入れることはできません。よって、その前のiまでの品物から選んだ時の価値の最大値に等しくなります。したがってdp[i, w] = dp[i-1, w]となります。
• もしw >= Weight[i]ならばi番目の品物を入れることができます。すると、入れない場合の最大値dp[i-1, w]と入れる場合の最大値dp[i-1, w-Weight[i]] + Value[i]を比べて大きい方の値がdp[i, w]となります。入れる場合の最大値は少々分かりにくいですが、dp[i-1, w-Weight[i]]はWeight[i]だけ余裕がある状況の価値の最大値であり、そこにi番目の品物（価値Value[i]）を入れるのでdp[i-1, w-Weight[i]] + Value[i]になります。

例題の数字を使って、dp[3, 4]を決めている状況が以下の図になります（蟻本のp.55から引用）。i = 3なので(Weight, Value) = (3, 4)です。よってdp[3, 4] = max(dp[2, 4], dp[2, 4-Weight[i]]) + Value[i] = max(5, 2+4) = 6となります。

このままdpテーブルを全て埋めてdp[N, Max_W]を求めると、それがナップサック問題の解となります。

---

以上は自分用の備忘録でした。以下では次のような問題を考えます。

上記のファイルのように重さはすべて既知である30個の品物があるとします。価値についてはそのうち25個しか分かっていません。ここで、あるブラックボックスの自然現象のルールがあって、30個の品物から重さの総和が40を超えないように選んで、価値を最大化すると考えられています。そして、最大化された価値を8回測定しました。結果は測定誤差を含めて、Y <- c(63.1, 66.8, 72.5, 58.1, 55.2, 67.5, 69.1, 70.2)でした。この結果から未知である5つの品物の価値の（事後）分布を推定することを考えます。ただし、価値の事前分布をnormal(3, 5)とします。

この問題はナップサック問題の逆問題のようになっています。Stanでの実装例は以下になりました。

• 2～15行目：冒頭で説明したアルゴリズムを実装しています。ただし、Stanの配列はインデックスが1からはじまるので、2次元配列dp[,]に関係するインデックスはすべて+1しています。
• 21, 23, 32行目：I_misは価値が未知の品物の個数、Idx_misはその品物のインデックス（ここでは26～30）、v_misはその品物のそれぞれの価値（パラメータ）です。
• 37～43行目：価値の分からない品物を混ぜた状態で、価値を最大化してmuに代入しています。
• 48行目：muに測定誤差が加わって観測したデータYになっています。

実行するRコードは以下の通りです。

推定結果は以下になりました。

	mean	se_mean	sd	2.5%	25%	50%	75%	97.5%	n_eff	Rhat
v_mis[1]	5.88	0.09	4.21	0.38	2.63	5.07	8.17	16.27	2294	1.00
v_mis[2]	5.18	0.09	3.60	0.27	2.29	4.57	7.47	13.28	1628	1.00
v_mis[3]	9.87	0.13	4.54	0.85	6.97	10.16	13.02	18.26	1202	1.00
v_mis[4]	7.75	0.13	5.05	0.23	3.51	7.19	11.59	17.65	1454	1.00
v_mis[5]	10.67	0.10	4.08	2.65	7.83	10.73	13.40	18.61	1567	1.00
s_Y	8.07	0.08	3.22	4.30	5.88	7.31	9.35	16.55	1594	1.00
mu	62.69	0.06	3.17	55.12	61.06	63.14	64.83	67.67	2652	1.00
lp__	-13.70	0.07	2.19	-18.59	-14.95	-13.34	-12.06	-10.49	861	1.00

測定で得られたYの値はかなり高いので、28と30番目の品物（それぞれv_mis[3]とv_mis[5]）が価値最大化の品物リストに加わる可能性が高く、ともに事後平均が10ぐらいになっています。

ちなみにナップサック問題のバリエーションには以下のものがあるようです。解き方は一例です。

• 各品物の個数が無限個の場合、あるいは個数に制限がある場合。→漸化式を工夫して解く（蟻本のp.58, p.302）
• 重さが連続値で価値が整数値の場合。→dp[i, v]を「i番目までの品物から価値の総和がvとなるように選んだときの、重さの総和の最小値（そのような解が存在しない場合は十分大きな値INF）」と定義する（蟻本のp.60）。
• 各品物の重さと価値が連続量の場合。→僕が調べた限りでは、枝刈りとかで地道に探索するかないっぽい…。詳しい人いましたら教えてください。
• 各品物を液体とし、個数が離散値ではなく好きな量だけ入れることができる連続値の場合。→東北大の塩浦先生の資料が詳しかったです(pdf)。

人口ピラミッドのAge Heapingを階層ベイズで補正する

1週間ぐらい前に以下のツイートがバズっていました。togetterのまとめはこちら。

インドネシアの人口ピラミッド、どうしてこうなったのか
自分の年齢を気にしない文化なのか pic.twitter.com/yPcvUCkpD2

— やなせ (@ynsitx) 2016年6月16日

このグラフのソースは恐らく以下の西文彦氏による文書です。

統計局ホームページ/統計に関する国際協力/国際協力・交流/インドネシア中央統計庁（BPS）に対する技術協力

Age Heapingの解説がありますので引用します。

Age Heaping（エイジ・ヒーピング）とは、図1に見られるように、人口ピラミッドなどの年齢各歳別の統計において、例えば50 歳、55歳など、0または5で終わる年齢において、人口が突出して多くなる現象のことである。 この現象が起こる原因は、その国において、自分の年齢を正確に知らない人が多いことである。このため、自分の年齢を回答する場合には、50歳、55歳などと、自分の年齢に近いと思われる、切りの良い数字で回答することになるわけである。 この現象は、発展途上国に多く見られる。ただし、発展途上国であっても、十二支が社会的習慣として浸透している国では、この現象は見られない。

干支なんて不要と思っていましたが、こんなメリットがあるとは…。また、統計調査などで回答された年齢の正確さを測定するための指標の一つとしてMyers' Index（マイヤーズ・インデックス）というものがあるそうです。Rで算出する例はこちらのWebにありました。

この記事では階層ベイズで真の*1構成比率を推定することで、冒頭の1990年のインドネシアの人口ピラミッドを補正したいと思います。データは国連の統計情報データベースから取得しました。人口ピラミッドを描くと以下になりました。

西氏の人口ピラミッドがほぼ再現されています（横軸の単位は万人）。なお、75歳のところは75歳以上を答えた人も含みます。

補正後の人口（構成比率）ピラミッド

今回は男女別々に推定してみました。推定に使用したStanコードとRコードの解説は記事の最後にあります。補正後の人口（構成比率）ピラミッドは以下になります。

棒グラフの値は推定で得たMCMCサンプルの中央値で、エラーバーは95%ベイズ信頼区間です。横軸は人口ではなく、性別ごとの構成比率（人口/性別ごとの人口の合計値, 単位は%）にしてあります。

元データと比較した図は以下になります。

棒グラフの値はデータから算出した構成比率で、折れ線グラフの値は推定で得たMCMCサンプルの中央値です。18歳未満や75歳（75歳以上を含む）は補正の影響は少ないですが、それ以外の部分はかなり補正されています。

各性別・各年齢における真の年齢ではないキリのよい数字に回答する割合

各性別・各年齢において、どれくらいの人が年齢をテキトーに回答するか（真の年齢ではないキリのよい数字に回答するか）の割合を表した図が以下になります。

点は推定で得たMCMCサンプルの中央値で、エラーバーは95%ベイズ信頼区間です。一見、男女差はあまりなさそうです。高年齢のほうがテキトーに回答する割合がアップする傾向があると解釈できます。ただし、エラーバーは大きくなっています。また、19歳と30歳・40歳・50歳・60歳の前後一歳の値も比較的大きくなっています。なかなか興味深いです。

---

Stanコードは以下です。

• 2行目： 年齢の数です。今回は0～75の76になります。
• 3行目： 各年齢における人口です。
• 4～6行目： テキトーに回答する年齢の数です。Fromの年齢のインデックスからToの年齢のインデックスへ流出があると考えます。このデータをR側で作っておくと、20～23行目のようにシンプルに記述できます。
• 10行目： 各年齢における真の構成比率です。合計すると1なのでsimplexで宣言しています。
• 11行目： qに対して2階階差のマルコフ場モデルを使って滑らかさを仮定します。その滑らかさを決めるパラメータです。
• 28行目： マルコフ場モデルです。状態空間モデルと式の形は同じです（この記事や岩波DS1を参照）。75歳のqは75歳以上も含んでいるのでそこは避けて滑らかさを仮定する必要があります。そこでq[A]はこの式から意図的に外してあります。
• 12～14行目： r[j]はFrom[j]の年齢の人のうち、テキトーに回答する割合です。
• 26～27行目： rには正規分布を仮定し、mu_rとs_rはデータから推定します。すなわち階層ベイズになっています。rは[0,1]の範囲の値をとるパラメータであるため、27行目は切断正規分布になっています。切断正規分布がパラメータを含む場合は、正規化の部分の尤度を考慮する必要があります（Stanのマニュアルの「6. Regression Models」の章のTruncated Priorsの節を参照）。ここでは-log(Phi((1-mu_r)/s_r) - Phi((0-mu_r)/s_r))の分の尤度を加える必要があります。これをStanの関数で少しだけ安定な形に書き直したものが28行目です。なお、rに関してはじめは、真の年齢から-2歳で答える割合、-1歳で答える割合、+1歳で答える割合、+2歳で答える割合の4種類だけ考えて、どの年代でも共通のパラメータにしていたのですが、このデータでは明らかに18歳未満がそれ以上と異なる挙動なのでうまくいきませんでした。見た目では明らかな挙動の変化がないような他の国のデータでも試してみましたが、やはり階層ベイズにして柔らかく仮定しないとうまくいきませんでした。
• 18行目： muは流出を含めたあとの構成比率です。合計すると1になっています。
• 29行目： このmuをパラメータとした多項分布で各年齢における人口データYが生成されると考えました。なお、Stanの多項分布は確率だけ指定すればよくて、合計の試行数はデータから自動的に算出されます。

実行するRコードは以下です。

• 3～5行目： 13・15行目でStanのJ・From・Toに流出元と流出先の年齢のインデックスを渡すために、ここでそのデータを作成しています。キリの良い数字は0歳から75歳までの5歳刻みです。

今回はキリの良い数字からその他の数字への流出は無視しました。また、最も近いキリのよい数字に回答することだけを考慮しました。すなわち、12歳からは10歳への流出だけ、13歳は15歳への流出だけを考慮しました。このあたりは変更の余地はあると思います。

計算時間はSurface Pro 3 (Core i5)で1chainあたり200秒ぐらいでした。バッチリ収束しました。

• 追記

人口ピラミッドの描き方はこちらを参考にしました。

*1:厳密には、モデルが正しいと仮定した場合の、真の。