1週間ぐらい前に以下のツイートがバズっていました。togetterのまとめはこちら。
インドネシアの人口ピラミッド、どうしてこうなったのか
— やなせ (@ynsitx) 2016年6月16日
自分の年齢を気にしない文化なのか pic.twitter.com/yPcvUCkpD2
このグラフのソースは恐らく以下の西文彦氏による文書です。
統計局ホームページ/統計に関する国際協力/国際協力・交流/インドネシア中央統計庁(BPS)に対する技術協力
Age Heapingの解説がありますので引用します。
Age Heaping(エイジ・ヒーピング)とは、図1に見られるように、人口ピラミッドなどの年齢各歳別の統計において、例えば50 歳、55歳など、0または5で終わる年齢において、人口が突出して多くなる現象のことである。 この現象が起こる原因は、その国において、自分の年齢を正確に知らない人が多いことである。このため、自分の年齢を回答する場合には、50歳、55歳などと、自分の年齢に近いと思われる、切りの良い数字で回答することになるわけである。 この現象は、発展途上国に多く見られる。ただし、発展途上国であっても、十二支が社会的習慣として浸透している国では、この現象は見られない。
干支なんて不要と思っていましたが、こんなメリットがあるとは…。また、統計調査などで回答された年齢の正確さを測定するための指標の一つとしてMyers' Index(マイヤーズ・インデックス)というものがあるそうです。Rで算出する例はこちらのWebにありました。
この記事では階層ベイズで真の*1構成比率を推定することで、冒頭の1990年のインドネシアの人口ピラミッドを補正したいと思います。データは国連の統計情報データベースから取得しました。人口ピラミッドを描くと以下になりました。
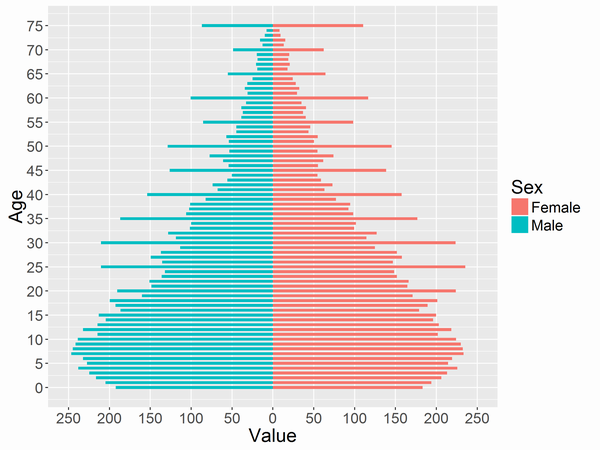
西氏の人口ピラミッドがほぼ再現されています(横軸の単位は万人)。なお、75歳のところは75歳以上を答えた人も含みます。
補正後の人口(構成比率)ピラミッド
今回は男女別々に推定してみました。推定に使用したStanコードとRコードの解説は記事の最後にあります。補正後の人口(構成比率)ピラミッドは以下になります。
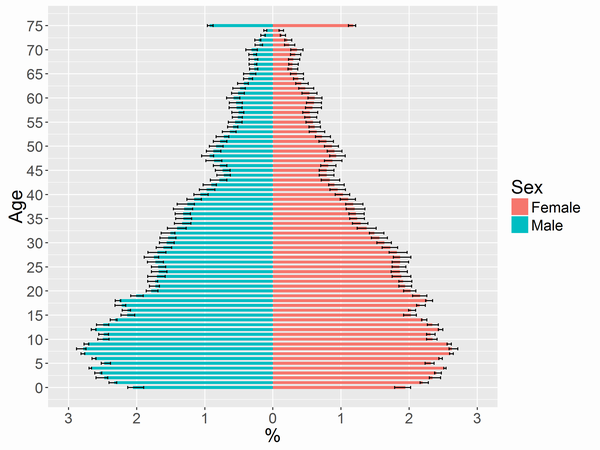
棒グラフの値は推定で得たMCMCサンプルの中央値で、エラーバーは95%ベイズ信頼区間です。横軸は人口ではなく、性別ごとの構成比率(人口/性別ごとの人口の合計値, 単位は%)にしてあります。
元データと比較した図は以下になります。
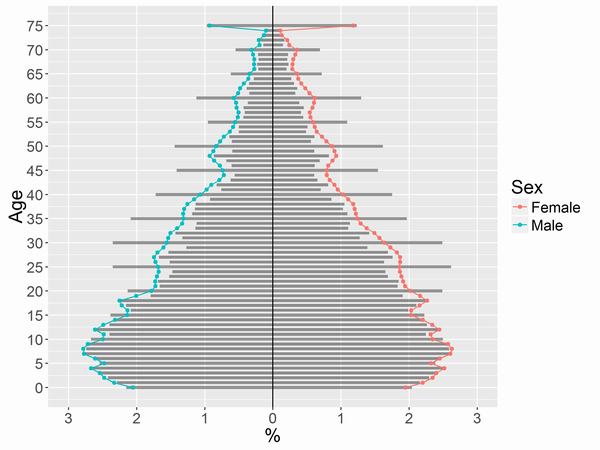
棒グラフの値はデータから算出した構成比率で、折れ線グラフの値は推定で得たMCMCサンプルの中央値です。18歳未満や75歳(75歳以上を含む)は補正の影響は少ないですが、それ以外の部分はかなり補正されています。
各性別・各年齢における真の年齢ではないキリのよい数字に回答する割合
各性別・各年齢において、どれくらいの人が年齢をテキトーに回答するか(真の年齢ではないキリのよい数字に回答するか)の割合を表した図が以下になります。
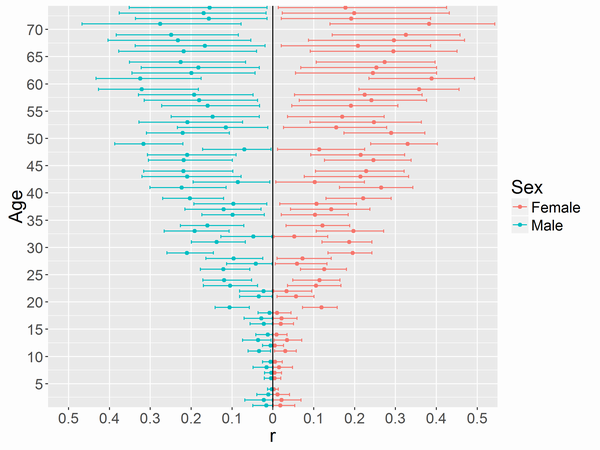
点は推定で得たMCMCサンプルの中央値で、エラーバーは95%ベイズ信頼区間です。一見、男女差はあまりなさそうです。高年齢のほうがテキトーに回答する割合がアップする傾向があると解釈できます。ただし、エラーバーは大きくなっています。また、19歳と30歳・40歳・50歳・60歳の前後一歳の値も比較的大きくなっています。なかなか興味深いです。
Stanコードは以下です。
- 2行目: 年齢の数です。今回は0~75の76になります。
- 3行目: 各年齢における人口です。
- 4~6行目: テキトーに回答する年齢の数です。
Fromの年齢のインデックスからToの年齢のインデックスへ流出があると考えます。このデータをR側で作っておくと、20~23行目のようにシンプルに記述できます。 - 10行目: 各年齢における真の構成比率です。合計すると1なので
simplexで宣言しています。 - 11行目:
qに対して2階階差のマルコフ場モデルを使って滑らかさを仮定します。その滑らかさを決めるパラメータです。 - 28行目: マルコフ場モデルです。状態空間モデルと式の形は同じです(この記事や岩波DS1を参照)。75歳の
qは75歳以上も含んでいるのでそこは避けて滑らかさを仮定する必要があります。そこでq[A]はこの式から意図的に外してあります。 - 12~14行目:
r[j]はFrom[j]の年齢の人のうち、テキトーに回答する割合です。 - 26~27行目:
rには正規分布を仮定し、mu_rとs_rはデータから推定します。すなわち階層ベイズになっています。rは[0,1]の範囲の値をとるパラメータであるため、27行目は切断正規分布になっています。切断正規分布がパラメータを含む場合は、正規化の部分の尤度を考慮する必要があります(Stanのマニュアルの「6. Regression Models」の章のTruncated Priorsの節を参照)。ここでは-log(Phi((1-mu_r)/s_r) - Phi((0-mu_r)/s_r))の分の尤度を加える必要があります。これをStanの関数で少しだけ安定な形に書き直したものが28行目です。なお、rに関してはじめは、真の年齢から-2歳で答える割合、-1歳で答える割合、+1歳で答える割合、+2歳で答える割合の4種類だけ考えて、どの年代でも共通のパラメータにしていたのですが、このデータでは明らかに18歳未満がそれ以上と異なる挙動なのでうまくいきませんでした。見た目では明らかな挙動の変化がないような他の国のデータでも試してみましたが、やはり階層ベイズにして柔らかく仮定しないとうまくいきませんでした。 - 18行目:
muは流出を含めたあとの構成比率です。合計すると1になっています。 - 29行目: この
muをパラメータとした多項分布で各年齢における人口データYが生成されると考えました。なお、Stanの多項分布は確率だけ指定すればよくて、合計の試行数はデータから自動的に算出されます。
実行するRコードは以下です。
- 3~5行目: 13・15行目でStanの
J・From・Toに流出元と流出先の年齢のインデックスを渡すために、ここでそのデータを作成しています。キリの良い数字は0歳から75歳までの5歳刻みです。
今回はキリの良い数字からその他の数字への流出は無視しました。また、最も近いキリのよい数字に回答することだけを考慮しました。すなわち、12歳からは10歳への流出だけ、13歳は15歳への流出だけを考慮しました。このあたりは変更の余地はあると思います。
計算時間はSurface Pro 3 (Core i5)で1chainあたり200秒ぐらいでした。バッチリ収束しました。
- 追記
*1:厳密には、モデルが正しいと仮定した場合の、真の。