「Tutorial 6: Mixture of Gaussians」をやります。みんな大好き混合正規分布です。
infer.netの例題は分散小さめな2つの正規分布がかなり離れており、点も混じることなくつまらないのでサンプルデータの作成部分を少しいじりました。まず二変量正規分布が2つ混ざる部分のデータ作成部分は以下になります。
library(MASS) library(mvtnorm) set.seed(123) get.example.df <- function(n, mu1, mu2, s1, s2, p1){ dice <- sample(c(0,1), n, replace=T, prob=c(p1, 1-p1)) n1 <- sum(dice == 0) n2 <- n - n1 df <- rbind(cbind(mvrnorm(n1, mu1, s1), rep(1, n1)), cbind(mvrnorm(n2, mu2, s2), rep(2, n2))) df <- data.frame(df) colnames(df) <- c("x1", "x2", "k") df } MixtureModelDens <- function(x1, x2, m1, m2, s1, s2, pi1, pi2){ f1 <- function(x1, x2){ dmvnorm(matrix(c(x1, x2), ncol=2), mean=m1, sigma=s1) } f2 <- function(x1, x2){ dmvnorm(matrix(c(x1, x2), ncol=2), mean=m2, sigma=s2) } z1 <- outer(x1, x2, f1) z2 <- outer(x1, x2, f2) pi1*z1 + pi2*z2 } mu1 <- c(2, 3) s1 <- solve(matrix(c(2, 0.2, 0.2, 1), 2, 2)) mu2 <- c(4, 5) s2 <- solve(matrix(c(1.5, 0.4, 0.4, 2), 2, 2)) true.pi <- 0.6 N <- 300 Y.df <- get.example.df(N, mu1, mu2, s1, s2, true.pi) Y <- as.matrix(Y.df[,-3]) x1 <- seq(from=0, to=8, length=100) x2 <- x1 z <- MixtureModelDens(x1, x2, mu1, mu2, s1, s2, true.pi, 1-true.pi) png("output/example_data.png", h=400, w=400) image(x = x1, y = x2, z = z, zlim = c(0, 0.25), col = grey(99:0/100)) Y1 <- subset(Y.df, 1==k) Y2 <- subset(Y.df, 2==k) points(Y1[,1], Y1[,2], pch=20, col = rgb(0,0,1, alpha=0.3)) points(Y2[,1], Y2[,2], pch=20, col = rgb(1,0,0, alpha=0.3)) dev.off()
24行目、26行目ではinfer.netの例題を参考に精度行列を作って、その逆行列を求めることで分散共分散行列を得ています。MixtureModelDens()関数は「Rで混合正規分布を描く。 - Analyze IT.」からほぼ拝借しました。データを生成した真の混合分布とデータ点はこんな感じです。
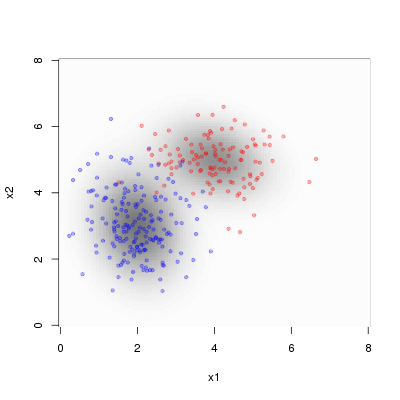
青点・赤点の色の違いはどちらの二変量正規分布から生成されたかを表しています。推定したいものは、2つの二変量正規分布の平均ベクトルと精度行列、そして混ぜ具合であるtrue.piになります。
BUGSコードは何も考えずに書くと以下になりました。
model { for (i in 1:N){ Y[i, 1:N.dim] ~ dmnorm(mn[z[i],], tau[z[i],,]) z[i] ~ dcat(p[]) } p[1:K] ~ ddirch(Theta[]) for (k in 1:K){ mn[k, 1:N.dim] ~ dmnorm(Zero[], Non.informative.tau[,]) tau[k, 1:N.dim, 1:N.dim] ~ dwish(R[,], 100) } }
実はBUGSなどのMCMC系のオーソドックスなサンプリング方法ではこの手の問題が一筋縄でいかないことが知られています。上記のように2つの二変量正規分布の平均ベクトルをある分布から生成するようにすると、mixingがうまく行かなくなり、2つの平均ベクトルが同じものになってしまい、true.piは0か1になってしまいます。このあたりは「The BUGS Book 11.6 Finite mixture and latent class models」に記述があります。これを避けるには、パラメータ化を工夫しなくてはなりません。今回は以下のように工夫しました。
model { for (i in 1:N){ Y[i, 1:N.dim] ~ dmnorm(mn[z[i],], tau[z[i],,]) z[i] ~ dcat(p[]) } p[1:K] ~ ddirch(Theta[]) for (k in 1:K){ tau[k, 1:N.dim, 1:N.dim] ~ dwish(R[,], 100) var.cov[k, 1:N.dim, 1:N.dim] <- inverse(tau[k,,]) } for (d in 1:N.dim){ mn[1, d] <- center[d] + xi[d] mn[2, d] <- center[d] - xi[d] } center[1:N.dim] ~ dmnorm(Zero[], Non.informative.tau[,]) xi[1] <- len * cos(rad) xi[2] <- len * sin(rad) len ~ dnorm(0, 1.0E-4) rad ~ dunif(-3.141592, 3.141592) }
2つの平均ベクトルを直線でつないで、その中心をcenterとしています。あとは極座標の要領で決めます。唯一苦労したところは、19行目になりまして、はじめは極座標の半径部分(len)は正の値を一様分布で渡していたのですがTrapが止まりませんでした。そこでマイナスもOKのように正規分布を使った無情報事前分布にしたところ、うまくいきました。
キックするRコードは以下になります。
#...データ作成部分... N.dim <- 2 K <- 2 source("R2WBwrapper.R") clear.data.param() set.data("N", N) set.data("K", K) set.data("N.dim", N.dim) set.data("Y", Y) set.data("Theta", rep(1, K)) set.data("Zero", rep(0, N.dim)) set.data("Non.informative.tau", diag(rep(1.0E-4, N.dim), N.dim)) set.data("R", diag(rep(0.5, N.dim), N.dim)) z.ini <- ifelse(Y[,2] < mean(Y[,2]), 1, 2) set.param("z", z.ini, save=F) set.param("p", rep(0.5, K)) set.param("center", mvrnorm(1, colMeans(Y), diag(rep(1, N.dim)))) set.param("len", runif(1, -10, 10)) set.param("rad", runif(1, -pi, pi)) tau.tmp <- array(rep(diag(rep(10, N.dim)), K), dim=c(N.dim, N.dim, K)) tau.ini <- aperm(tau.tmp, perm=c(3,1,2)) set.param("tau", tau.ini) set.param("mn", NA) set.param("var.cov", NA) post.bugs <- call.bugs( n.chains = 3, file = "model.bugs", n.iter = 10000, n.burnin = 2000, n.thin = 40 ) post.list <- to.list(post.bugs) post.mcmc <- to.mcmc(post.bugs) save.image("output/result.RData")
あと、この問題は初期値を結構頑張って設定しないと収束しません。特にzがランダムだとNGです(17-18行目)。tauの初期値は対角行列を2つ与えたいだけなのですが、BUGSの文法の制限より添え字の順番が固定されていまして、ややこしくなってしまっています(23-25行目)。
結果は以下の通りです。
| mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | Rhat | n.eff | |
|---|---|---|---|---|---|---|---|---|---|
| p[1] | 0.56 | 0.03 | 0.50 | 0.54 | 0.56 | 0.58 | 0.62 | 1.00 | 600 |
| p[2] | 0.44 | 0.03 | 0.38 | 0.42 | 0.44 | 0.46 | 0.50 | 1.00 | 600 |
| center[1] | 2.90 | 0.06 | 2.80 | 2.87 | 2.90 | 2.94 | 3.01 | 1.00 | 340 |
| center[2] | 3.93 | 0.05 | 3.83 | 3.90 | 3.93 | 3.97 | 4.03 | 1.00 | 600 |
| len | -1.40 | 0.03 | -1.46 | -1.42 | -1.40 | -1.37 | -1.33 | 1.00 | 600 |
| rad | 0.77 | 0.04 | 0.71 | 0.75 | 0.77 | 0.80 | 0.85 | 1.00 | 560 |
| tau[1,1,1] | 3.88 | 0.42 | 3.01 | 3.61 | 3.89 | 4.15 | 4.72 | 1.01 | 160 |
| tau[1,1,2] | 0.89 | 0.26 | 0.40 | 0.72 | 0.89 | 1.06 | 1.38 | 1.01 | 590 |
| tau[1,2,1] | 0.89 | 0.26 | 0.40 | 0.72 | 0.89 | 1.06 | 1.38 | 1.01 | 590 |
| tau[1,2,2] | 2.26 | 0.33 | 1.71 | 2.03 | 2.24 | 2.47 | 2.92 | 1.00 | 600 |
| tau[2,1,1] | 1.96 | 0.29 | 1.42 | 1.75 | 1.95 | 2.16 | 2.60 | 1.00 | 600 |
| tau[2,1,2] | 0.17 | 0.20 | -0.20 | 0.03 | 0.15 | 0.31 | 0.59 | 1.00 | 340 |
| tau[2,2,1] | 0.17 | 0.20 | -0.20 | 0.03 | 0.15 | 0.31 | 0.59 | 1.00 | 340 |
| tau[2,2,2] | 3.76 | 0.45 | 2.99 | 3.47 | 3.71 | 4.04 | 4.75 | 1.01 | 150 |
| mn[1,1] | 1.91 | 0.05 | 1.82 | 1.87 | 1.90 | 1.94 | 2.01 | 1.01 | 250 |
| mn[1,2] | 2.96 | 0.07 | 2.82 | 2.91 | 2.96 | 3.00 | 3.10 | 1.00 | 600 |
| mn[2,1] | 3.90 | 0.09 | 3.71 | 3.84 | 3.90 | 3.96 | 4.08 | 1.00 | 590 |
| mn[2,2] | 4.91 | 0.05 | 4.80 | 4.88 | 4.91 | 4.94 | 5.00 | 1.00 | 470 |
| var.cov[1,1,1] | 0.29 | 0.03 | 0.24 | 0.27 | 0.29 | 0.30 | 0.35 | 1.01 | 200 |
| var.cov[1,1,2] | -0.11 | 0.03 | -0.16 | -0.13 | -0.11 | -0.09 | -0.06 | 1.00 | 600 |
| var.cov[1,2,1] | -0.11 | 0.03 | -0.16 | -0.13 | -0.11 | -0.09 | -0.06 | 1.00 | 600 |
| var.cov[1,2,2] | 0.50 | 0.06 | 0.39 | 0.45 | 0.49 | 0.54 | 0.63 | 1.00 | 600 |
| var.cov[2,1,1] | 0.53 | 0.08 | 0.39 | 0.47 | 0.52 | 0.58 | 0.71 | 1.00 | 600 |
| var.cov[2,1,2] | -0.02 | 0.03 | -0.08 | -0.04 | -0.02 | 0.00 | 0.03 | 1.00 | 600 |
| var.cov[2,2,1] | -0.02 | 0.03 | -0.08 | -0.04 | -0.02 | 0.00 | 0.03 | 1.00 | 600 |
| var.cov[2,2,2] | 0.27 | 0.03 | 0.21 | 0.25 | 0.27 | 0.29 | 0.34 | 1.01 | 160 |
2つの二変量正規分布の平均ベクトルと混ぜ具合であるp[1]はほぼ真の値が推定されていますが、精度行列が少し異なります。これはデータがどちらの二変量正規分布由来か区別つかない状態で与えていますので、入り混じっているところの点が平均ベクトルに近いほうから生成されている確率が高いとみなされていることに起因します。得られたMCMCサンプルから、推定された混合分布を描きますと以下のようになりました(データの青点・赤点は比較のためオリジナルのまま)。
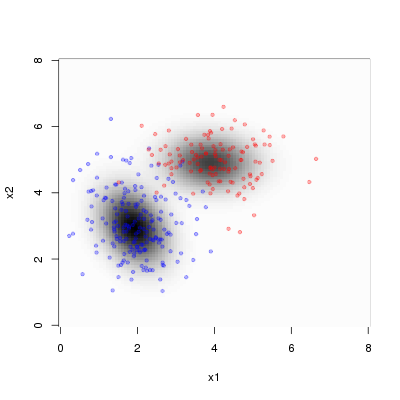
さて、さらに調子のってリング状に分布しているデータに対して、7つの二変量正規分布で推定するという問題に着手しました。データ作成部分は以下。
set.seed(123) N <- 1000 r <- 0.1 + 0.2 * runif(N) theta <- 2 * pi * runif(N) d <- data.frame(x=r*cos(theta)+0.5, y=r*sin(theta)+0.5) write.table(d, file="input/data.txt", quote=F, row.names=F, sep="\t")
実はこの問題を過去にrubyでEMアルゴリズムを実装して解いたことがあります。データおよびアルゴリズムはBishop先生の名著「Neural Networks for Pattern Recognition」の 「2.6 Mixture models」 p.68を参考にしたものです。この本を劣化縮小したものがPRMLの5章になっております。この本はEMアルゴリズム、ヘシアンを使った最適化部分、ニューラルネットの基礎などが懇切丁寧に解説されており今でも色あせてないと思います。また実装面にも的確な記述があり、PRMLよりも実際にプログラミングして鍛えるのに向いていると思います。

Neural Networks for Pattern Recognition (Advanced Texts in Econometrics (Paperback))
- 作者:Bishop, Christopher M.
- 発売日: 1996/01/18
- メディア: ペーパーバック
以下がrubyコードになります。NArray使いまくりです。rubyがあれば何でも分析できる、そんなふうに考えていた時期が僕にもありました。
require 'narray' dat_a = File.foreach("input/data.txt").each_with_index.inject([]) do |ar, (line, ix)| next ar if ix.zero? ar << line.chomp.split("\t").map{|x| x.to_f } end ELE_N = 7 DIM_N = 2 DAT_N = 1000 NArray.srand(3) dat_na = NArray.to_na(dat_a) # 2次元データベクトル [x,y] x1000. 添え字は n=1..1000 m_na = NArray.float(DIM_N,ELE_N).randomn + 0.5 # 2次元平均ベクトル [xm,ym] が j個(混合分布を形成するガウス分布の数) s2_na = NArray.float(ELE_N).randomn.abs # 分散 s2 が j個(混合分布を形成するガウス分布の数) p_j = NArray.float(ELE_N).fill!(1.0/ELE_N) # 混合分布j個の事前確率 ## P(j|x[n]) = P(x[n]|j) * p_j / p(x[n]) を求める. # 1. p_jは初期値あり. # 2. p(x[n])は Sum[ P(x[n]|j) * p_j, n=1..1000] でP(x[n]|j)とp_jから作る. # 3. P(x[n]|j)は 多変量正規分布(今回は分散共分散行列は対角行列)から算出. p_x = NArray.float(DAT_N) # p(x[n]) p_j_cond = NArray.float(ELE_N,DAT_N) # p(x[n]|j) p_xn_cond = NArray.float(ELE_N,DAT_N) # P(j|x[n]) p_xn_cond_sum = NArray.float(ELE_N) 100.times do |loop| # P(x[n]|j)を作る DAT_N.times do |n| ELE_N.times do |j| tmp_na = dat_na[true,n] - m_na[true,j] p_j_cond[j,n] = 1.0/(2*Math::PI*s2_na[j])*Math.exp(-tmp_na.mul_add(tmp_na,0)/2.0/s2_na[j]) end end # p(x[n])を作る DAT_N.times do |n| p_x[n] = p_j_cond[true,n].mul_add(p_j,0) end # P(j|x[n])を作る DAT_N.times do |n| ELE_N.times do |j| p_xn_cond[j,n] = p_j_cond[j,n] * p_j[j] / p_x[n] end end # Sum[ P(j|x[n]), n=1..1000] ELE_N.times do |j| p_xn_cond_sum[j] = p_xn_cond[j,true].sum end # m_naの更新 ELE_N.times do |j| m_na[true,j] = p_xn_cond[j,true].mul_add(dat_na.transpose(1,0),0) / p_xn_cond_sum[j] end # s2_naの更新 ELE_N.times do |j| tmp_na = dat_na - m_na[true,j] s2_na[j] = 0.5 * p_xn_cond[j,true].mul_add(tmp_na.mul_add(tmp_na,0),0) / p_xn_cond_sum[j] end # p_jの更新 ELE_N.times do |j| p_j[j] = 1.0/DAT_N * p_xn_cond_sum[j] end end X_MESH = 120 Y_MESH = 120 out_aa = Y_MESH.times.map do |y_i| y = 1.0/(Y_MESH-1) * (Y_MESH-1-y_i) X_MESH.times.map do |x_i| x = 1.0/(X_MESH-1) * x_i na = NArray.to_na([x,y]) ELE_N.times.inject(0) do |sum, j| tmp_na = na - m_na[true,j] sum += p_j[j] * 1.0/(2*Math::PI*s2_na[j])*Math.exp(-tmp_na.mul_add(tmp_na,0)/2.0/s2_na[j]) end end end open("output/EM_result.txt", "w") do |fout| fout.puts out_aa.map{|x| x.join("\t") }.join("\n") end
最後のデータ出力はそのままexcelで開いて色をつけると左下が(0,0)で横軸がx軸、縦軸がy軸になるようにしています。結果の図は以下になります。青い点がデータ点です。なかなかうまく行っています。
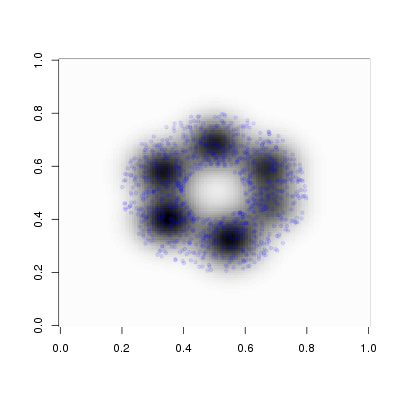
上の図の描き方は以下になります。image()関数は90度回転することを忘れていてハマりました(参考 3次元のデータをグラフにする - どんな鳥も)。備忘録として載せます。今なら{ggplot2}で書きます。
dens <- as.matrix(read.delim("output/EM_result.txt", sep="\t", as.is=T, header=F)) points <- read.delim("input/data.txt", sep="\t", as.is=T, header=T) png("output/EM_result.png", h=400, w=400) image(z = t(dens)[ ,nrow(dens):1], col = grey(99:0/100)) points(points$x, points$y, pch=20, col = rgb(0,0,1, alpha=0.1)) dev.off()
この問題をBUGSでいくぜぇぇぇと突撃したのですが、前述の通りMCMC系では苦手な問題であり爆死しました。特にcomponent(=正規分布の数)が多いときはダメです。特別なアルゴリズムが必要であることが示唆されています(The BUGS Book p.281参照)。ちなみに1次元上に多数の正規分布が重なっている場合には、JAGSにはdnormmix()という必殺技があります。でも多変量版のdmnormmix()は存在しないため、ここらで撤退しました。