StatModeling Memorandum

StatModeling Memorandum

StanとRとPythonでベイズ統計モデリングします. たまに書評.

状態空間モデルでシステムノイズに非ガウス分布（1次元の変化点検出）

Stan

北川本「時系列解析入門」14.4節の例題をやってみましたので途中経過の作業ログとして残します。

時系列解析入門

時系列解析入門

まずは失敗例から。

data {
   int N;
   real Y[N];
}

parameters {
   real mu[N];
   real<lower=0> s_y;
   real<lower=0> s_mu;
}

model {
   for (n in 1:N)
      Y[n] ~ normal(mu[n], s_y);
   for (n in 2:N)
      mu[n] ~ cauchy(mu[n-1], s_mu);
}

16行目でシステムノイズにCauchy分布を使っていますが、このモデルは全く収束しません。

これを解決するヒントはStanのマニュアルの「19. Optimizing Stan Code」（の「Reparameterizing the Cauchy」節）にあります。Cauchy分布では幹の部分をうろちょろするのと比べて裾の重い部分をうろちょろするのは相対的にステップサイズが小さくなるため、rejectが増えて時間がとてもかかるようになります。こういう状況を解消する方法がこの章にはいくつか載っています。これをうけての改良版が以下。

data {
   int N;
   real Y[N];
}

parameters {
   real mu0;
   real<lower=0> s_mu;
   real<lower=-pi()/2, upper=pi()/2> mu_unif[N-1];
   real<lower=0> s_y;
}

transformed parameters {
   real mu[N];
   mu[1] <- mu0;
   for (n in 2:N)
      mu[n] <- mu[n-1] + s_mu*tan(mu_unif[n-1]);
}

model {
   for (n in 1:N)
      Y[n] ~ normal(mu[n], s_y);
}
  • 9,16,17行目: 累積分布関数を使う方法でCauchy分布に従う乱数を発生させています。この一様分布に従う乱数（mu_unif）を代わりに推定します。

キックするRコードは以下です。

library(rstan)

set.seed(123)
N <- 400
mu.true <- as.vector(mapply(rep, c(0,1,-1,0), 100))
Y <- rnorm(n=N, mean=mu.true, sd=1)
data <- list(N=N, Y=Y)

stan_fit <- stan(file="model1.stan", pars=c('mu', 's_mu', 's_y'), data=data, iter=1200, warmup=200, seed=12345)
  • 4～8行目: データを作成しています。

計算時間は1chainあたり数分でした。Rhatはすべて<1.1です。推定結果は以下のとおりです。

f:id:StatModeling:20201107120623p:plain

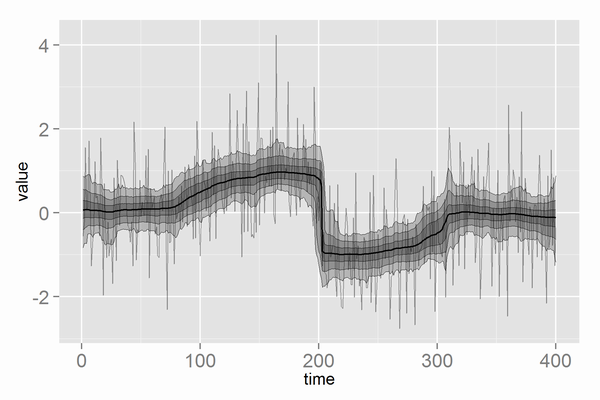
細い黒線で振動が激しいのが実データ、帯は外側から順にMCMCサンプルの99.9%信用区間、98%信用区間、85%信用区間です。真ん中の黒線はMCMCサンプルの中央値です。

さらに書籍に載っているコーシー分布より裾の重いピアソン分布族で実行したいです。これもモデルの組み方に工夫が必要でした。参考になったのは以下の書籍の9章です。web版を公開してくださっており大変感謝です。 Luc Devroye, "Non-Uniform Random Variate Generation", (SpringerVerlag, New York, 1986) この本によりますと欲しいピアソン分布族（VII）に従う乱数は以下の手順で生成できます（書籍の b-1/2 を b と置き換えています）。

f:id:StatModeling:20201107120611p:plain

f:id:StatModeling:20201107120614p:plain

f:id:StatModeling:20201107120619p:plain

これをそのまま実装したのが以下になります。

data {
   int N;
   real Y[N];
   real<lower=0> B;
}

parameters {
   real mu0;
   real<lower=0> s_mu;
   real<lower=0> s_y;
   real mu_raw1[N-1];
   real<lower=0> mu_raw2[N-1];
}

transformed parameters {
   real mu[N];
   mu[1] <- mu0;
   for (n in 2:N)
      mu[n] <- mu[n-1] + s_mu*mu_raw1[n-1]/sqrt(0.5*mu_raw2[n-1]);
}

model {
   for (n in 2:N){
      mu_raw1[n-1] ~ normal(0, 1);
      mu_raw2[n-1] ~ gamma(B, 1);
   }
   for (n in 1:N)
      Y[n] ~ normal(mu[n], s_y);
}
  • 4行目: ピアソン分布族のパラメータです。B=0.5の時がCauchy分布に対応します。

書籍の方ではB=0.1の結果があったのでそれを実行しました。計算時間は1chainあたり数分でRhatはすべて<1.1です。推定結果は以下のとおりです。

f:id:StatModeling:20201107120628p:plain

ちなみにBをパラメータとして推定させることもできました。その時はBの事後分布の中央値は0.81・平均値は0.79になりました。

追記