確率変数の変数変換とヤコビアンに慣れる
確率変数の変数変換においてヤコビアンを使う場合を簡単にまとめてみました。
●Q1. 以下は1.00…が出力されます。なぜですか？
sum <- 0 max <- 10000 for(i in 1:max){ sum <- sum + var(rnorm(5)) } print(sum/max)
10000回を十分大きな数とみなせば、これは変数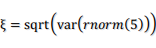
の平均値が出力されると解釈できます。ここで
は平均0, 標準偏差1の正規分布からランダムに抽出された5サンプルであることに注意して式変形すると、
となります。式の変形の途中にある
は母集団の標準偏差を表します。今回は1です。ここで、
は教科書に載っているように自由度4のカイ2乗分布に従います（この証明もそんなに難しくなく重要ですが今回はパスします）。また、自由度4のカイ2乗分布の平均値は4です。よって
の平均値
は、
となります。Q1.の最終的な出力は1となります。
●Q2. 以下は0.94…が出力されます。なぜですか？
sum <- 0 max <- 10000 for(i in 1:max){ sum <- sum + sqrt(var(rnorm(5))) } print(sum/max)
こちらも同様に変数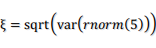の平均値が出力されると解釈できます。まずQ1と同様に式変形をします。
すると、今回は[
の平均を取ることが簡単にはできません。ですのできちんとの分布から計算します。さてが自由度4のカイ2乗分布に従う時、はどんな分布になるでしょうか？
この問いは「確率変数の変数変換」という確率・統計のオーソドックスな問題です。ちなみにカイ2乗分布やF分布やt分布やコーシー分布も、正規分布から抽出されたサンプルたちの、サンプルの値・サンプル数・母平均・母標準偏差・標本平均・標本標準偏差といったものを足したり引いたり掛けたり割ったりするうちにできた分布です。検定はそれらの分布を使っています。ただし、そのような変数変換はたいてい面倒くさいです。私のような実務家にとっては、目的はある問題を速く解くことにあります。その際は手計算などをすっとばしてブートストラップなどのシミュレーションでややこしい分布を求めることが一番よいこともしばしばです。しかし、今回のQ2.のようにしばしば“納得できない”ことがあります。そのような場合にはぜひ一度手計算で分布を求めてみるのがよいと思います。
変数変換のステップ
変数変換の基本アイデアは下の図の
が成り立つはずというものです。なので変換後の確率密度関数
になります。この
がの世界との世界の体積を測る目盛りの違いの補正のようなものです。ヤコビアン(Jacobian)と呼ばれます。
変数変換の具体的なステップですが以下のようになります。
であらわす（変換後を変換前で表す）
であらわす（変換前を変換後で表す）ヤコビアン
を求める。絶対値を取って正の値にします（正負の符号は座標軸の位置関係をあらわすものなので今は重要ではありません）。
を整理して終了。
では今回の場合の変数変換をやってみます。
- の分布が自由度4のカイ2乗分布:
なので、
で完成です（積分して1になることも示せます）。これが
の分布になります。下の図で■が自由度4のカイ2乗分布、■が自由度1のカイ2乗分布、■が
です。この図を見ると場合によっては正規分布で近似しても大丈夫そうなことも分かります。
さて最終的な出力はこのの平均値なので、平均値の定義より以下のように積分すれば求まります。
途中の＝の式変形はガンマ関数の定義の形に持っていきたいために以下のような変数変換をしています。
途中の＝の式変形はガンマ関数の定義を参照してください。 最終的な出力はQ2.のRの実行結果と一致します。
変数変換のステップ（逆関数が多価関数の場合）
1変数の場合でも逆関数が多価関数になる（値の範囲によって複数の関数がある）場合は注意が必要です。その場合は、
（
は全ての逆関数についての和）が成り立つと考えられるので、変数変換は、
となります。
例として、
が平均0・標準偏差1の正規分布に従うとき、
の分布の計算は以下のようになります。
最終的に自由度1のカイ2乗分布となります。
多価関数の例ではないですが、もう一つ調子に乗って
が任意の分布である時に、
で移した分布はどうなるでしょうか？
上記のステップに従って変換すると、
となり、
は [0,1]の一様分布 になることが分かります。さてここで
はp値と解釈できることを考えると、p値の分布は[0,1]の一様分布になることが分かります。この事実は多重検定の補正などに使われます（例えば測定項目が多い場合、p値をソートして横軸に順位、縦軸にp値をplotしてみて、p値が低い方の直線から外れているところからが本当に意味があるところと考えたりします）。
変数変換のステップ（2変数の場合）
2変数の場合のステップは以下のようになります。
というと
の同時分布が分かっているものとします。
を整理する。と
の同時分布
が得られる。- だけの分布が欲しいような場合はについて残りの変数を積分して消して終了。
最後の例として、大砲が弾をうってどれくらい遠くまで発射できるかの確率分布を求める問題を解いてみます。 出典:Stochastic Processes in Physics and Chemistry, Third Edition (North-Holland Personal Library) I.5節にある練習問題(p.19)
Q. 初速度、仰角
で大砲から弾を発射します。ここで、速度・仰角ともに、それぞれ
，
の周りに鋭い正規分布を取るとします（よって、負の値などは無視できるとします）。また空気の抵抗は無視できるとします。この時、弾の到達距離の分布はどのようなものになるでしょうか？
Answer. 垂直軸の移動距離の式
を解くと、着弾するまでの時間は
と分かります。すると、到達距離は
となります。よって、以下のような変数変換をします。
変換前を変換後で表すと、
ここで、 
です。微分の公式などがありますので使うと便利な時があります。
ヤコビアンは以下になります。
いま とが独立と考えられるので、
の同時分布は、
になります。
よって
の同時分布は、
になります。最終的に求めたいの分布は、ここからを積分して消去します。
この積分は解析的には（≒手計算では）解けませんので数値的に積分します。ここで、
として実行した結果が以下になります。横軸が到達距離、縦軸（奥行き）がパラメータ
を
の範囲で変えたもの、垂直軸（高さ）がを決めたときの到達距離の確率分布をあらわします。
で最も遠くまで飛ぶのはいつも通りですが、分布が少し右に尾を引いているのが分かります。
