StatModeling Memorandum

StatModeling Memorandum

StanとRとPythonでベイズ統計モデリングします. たまに書評.

underdispersion（過小分散）な場合のポアソン分布の代替

R Stan

overdispersion（過分散）なポアソン分布は個体差＆ポアソン分布で説明するのがシンプルで解釈しやすくて、個人的には好みです。ただ、個体差を考慮するモデルではunderdispersion（過小分散）の場合に対応できません。そのような場合には「ほぼ確定的な値が存在し、そこから外れるメカニズムをきちんと組み入れたモデル」がよさそうと思うのですが、まだ思案中です。

この記事では、overdispersion（過分散）な場合のポアソン分布の代替として、Rから簡単に使える4つの分布を紹介したいと思います。

分布の紹介とRからの使い方

超幾何分布（Hypergeometric distribution）

関数形は以下です（ N,K,n,y は非負の整数、以降の分布でも yの値域は同じ）。

K が N と比べて小さくて、 n が大きい時にPoisson分布になります。平均と分散は以下です。

合計 N 個のボールが入った壺があって、アタリのボールが K 個入っているとします。そして、ボールを1個ずつ取り出します。ただし、ボールは壺に戻しません。 n 個取り出したあとの、アタリのボールの個数 y の従う分布になっています。Rではプリインストールで関数が用意されています。

dhyper(x, m, n, k)

引数はWikipediaと少し異なります。xが確率変数の値、mがあたりのボールの個数（ K に対応）、nがはずれのボールの個数（ N-K に対応）、kが試行回数（ n に対応）です。いくつか分布を描くと以下になります（記法はWikipediaに揃えました）。

一般化ポアソン分布（generalized Poisson distribution, Lagrangian Poisson distribution）

Wikipediaのページは見つかりませんでした。関数形は以下です（ 0 \leq \theta 、 -1 \leq \lambda \leq 1）。

\lambda \lt 0の時にunderdispersionです。平均と分散は以下です。

詳しくは以下の論文を読むとよさそうだけど、有料なのでサラリーマンには入手が厳しいです。このあたりの説明を読むと待ち行列と密接な関係がありそうですが分かりません。

  • [2] Consul, P. C., & Jam, G. C. (1973a) A generalization of the Poisson distribution. Technometrics, 15, 791-799
  • [3] Consul, P. C., & Jam, G. C. (1973b) On some interesting properties of the generalized Poisson distribution. Biometrische Zeitschrift, 15, 495-500.
  • [4] Consul, P. C. (1989) Generalized Poisson Distributions: Properties and Applications. New York:　Marcel Dekker, Inc.

Rでは{RMKdiscrete}パッケージにあるdLGP関数を使います。

dLGP(x, theta, lambda)

いくつかunderdispersionの分布を描くと以下になります。

Conway-Maxwell-Poisson分布（Conway-Maxwell-Poisson distribution）

関数形は以下です（ 0 \leq \lambda 、 0 \leq \nu）。

和をとって正規化する必要があります。 1 \lt \nuの時にunderdispersionです。平均と分散は陽に表せず定義通りの式になるようです。

原論文が古くて入手が難しいです。Wikipediaの記述を読むと待ち行列と密接な関係がありそうですが分かりません。

  • [6] Conway, R. W.; Maxwell, W. L. (1962) A queuing model with state dependent service rates. Journal of Industrial Engineering, 12: 132–136

Rでは{CompGLM}パッケージにあるdcomp関数を使います。

dcomp(x, lam, nu)

いくつかunderdispersionの分布を描くと以下になります。

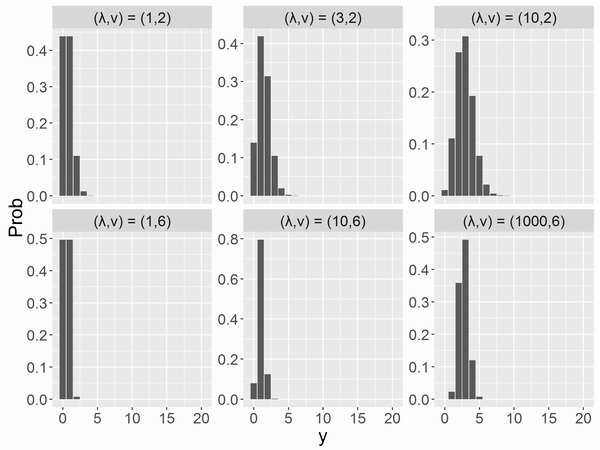
Double Poisson分布（double Poisson distribution）

Wikipediaのページは見つかりませんでした。関数形は以下です（ 0 \lt \mu 、 0 \lt \sigma）。

和をとって正規化する必要があります。 \sigma \lt 1の時にunderdispersionです。平均と分散は以下です（非常によい近似です）。

詳しくは以下の原論文（[7]と[8]）を読むとよいです（あのEfronです！）。一読したところ、exponential familyの拡張としてdouble exponential familyという分布族を定義して、そこにポアソン分布の確率質量関数を代入して整理すると出てくるようです。2次元の分割表にも関係しているようです。でも論文が難解で分かりませんでした。詳しい人いましたら教えてください。

  • [7] Efron, B., (1986) Double exponential families and their use in generalized linear Regression. Journal of the American Statistical Association 81 (395), 709-721. (link, preprint)
  • [8] Diaconis, P. & Efron, B. (1985) Rejoinder: Testing for Independence in a Two-Way Table: New Interpretations of the Chi-Square Statistic, Annals of Statistics, 13, 845–913. (link)
  • [9] Zou, Y., Geedipally, S.R. & Lord, D. (2013) Evaluating the Double Poisson Generalized Linear Model. Accident Analysis & Prevention, 59, 497–505 (link)

Rでは{gamlss.dist}パッケージにあるdDPO関数を使います(link)。

dDPO(x, mu, sigma)

いくつかunderdispersionの分布を描くと以下になります。

Stanを使って推定

デモデータは以下です。[10]のFig.1のAから逆算しました（厳密にはずれているかもしれません）。

  • [10] Kitazawa M. S., Fujimoto K. (2014) A Developmental basis for stochasticity in floral organ numbers Frontiers in Plant Science, 5, 545 (link)
  • [11] Kitazawa M. S., Fujimoto K. (2016) Relationship between the species-representative phenotype and intraspecific variation in Ranunculaceae floral organ and Asteraceae flower numbers. Annals of Botany. 117(5), 925-935 (link)

ある植物の個体ごとに花びらの数をカウントし、個体数を集計したものです。この後の論文（[11]）を読むと分かりますが、同じ種類の植物でも調査の場所によって分布がかなり異なるようです。もちろん植物の種類によっても分布は変わります。かなり面白いです。基本的にはoverdispersionの場合が多そうですが、ここではunderdispersionのデータを取り上げます。

本来は論文中に記述があるように、花びらの発生過程を考慮して分布を導くのがベストと思います。途中でerf関数が出てきますので、考察の基点は論文と異なりますが、分子の拡散現象と密接に関係しているのかなと思いました（次回の記事参照）。しかし、この記事ではそこまで深堀りしないで、単に上で紹介した超幾何分布を除く3つの分布をあてはめてみようとおもいます。

Stanコードだけ載せます。なお、どの分布も1chainあたり1秒以内に収束しました。

一般化ポアソン分布

推定結果はlambdaが境界値である-1にべったり張り付いていたので、モデルはダメそうです。この分布はデータのような激しいunderdispersionを表現できないのが原因と思います。

Conway-Maxwell-Poisson分布

上の式のままだと \lambda の値が大きくなりすぎてMCMCが非効率になります。そこで、[9]に記述がある以下の再パラメータ化をしました。

正規化項を別途計算しないといけないので少し複雑になっています。推定結果はmuとnuの中央値と95%ベイズ信頼区間がそれぞれ、5.65 [5.61, 5.68]と34.3 [31.6, 37.4]ほどになります。lambdaに直すと5.65^34.3ほどの値になりますので、データのような激しいunderdispersionにあてはめるのは厳しいのかもしれません。

なお、本来は確率質量関数を表すユーザ定義関数のsuffixは_log_likではなく_lpmfとするのが行儀よいですが、現在のStanのバージョンにはバグがあって、target +=と併せて使うことができません。次期バージョンでは直ります。

Double Poisson分布

正規化項を別途計算しないといけないので少し複雑になっています。推定結果はmuとsigmaの中央値と95%ベイズ信頼区間がそれぞれ、5.15 [5.12, 5.18]と0.03 [0.03, 0.03]ほどになります。個人的には、平均と分散をバラバラに変化させたい場合に、かなり自然にポアソン分布を2パラメータに拡張した分布になっているように思いました。

リアルデータ強い…