2次元以上のスポット検出を行う統計モデル
1次元の場合の変化点検出は以下の記事で扱いました。
- 状態空間モデルでシステムノイズに非ガウス分布(1次元の変化点検出) - StatModeling Memorandum
- 二つの時系列データの間に「差」があるか判断するには - StatModeling Memorandum
変化点検出のポイントは状態空間モデルのシステムモデルに「ほとんどの場合は0の近くの値を生成するが,まれにとても大きな値を生成する」という性質を持つ分布を使うことでした。そこで、上記の例ではコーシー分布を使いました。しかし、コーシー分布はかなり厄介な分布なので逆関数法を利用したコーディングをしないとうまくサンプリングできません。そのため2次元以上の場合の同様のモデル(マルコフ場モデル)に拡張することができません。2次元の場合のマルコフ場モデルについては以下の記事で簡単に扱いました(少しコードが古いです)。詳しくは書籍「StanとRでベイズ統計モデリング」の12章を参照してください。
それでも2次元以上のスポット検出を行いたくて色々なモデルを試しました。コーシー分布+実装の工夫、線過程(ライン過程)、混合正規分布、ベルヌーイ分布と正規分布の混合分布、両側指数分布(ラプラス分布)を使ったモデルなどなど。しかし、少なくとも私の環境においてはこれらのモデルだと、推定がうまくいかない場合や、推定できてもスポットのようにシャープではなくボワッと境界があいまいに推定されてしまう場合が多かったです。その後も2年にわたり粘り続けて合計150個弱のモデルを試した結果、一つの解決策を見つけましたのでこの記事を書きます。
UBN分布
アイデアは「ほとんどの場合は0の近くの値を生成するが,まれにとても大きな値を生成する」という性質を工夫して表現することです。そこで、状態空間モデルのシステムモデルに相当する部分に以下の分布を使いました。
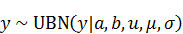
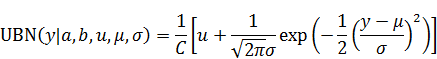
この分布は]の範囲の値を生成する、切断正規分布に一様分布のゲタをはかせたような分布です。ここで、
は一様分布の範囲を決めるパラメータ、
は一様分布のゲタの高さを決めるパラメータ、
は正規分布の平均と標準偏差、
は正規化項です。この分布は一様分布と切断正規分布の混合分布なのですが、ベルヌーイ分布とポアソン分布の混合分布をZero-inflated Poisson分布と分かりやすく呼ぶのになぞらえて、この記事では上記の分布をUniformly Boosted Normal Distributionと呼び、以下では略してUBN分布と呼びます。思いつけばコロンブスの卵ですが、UBN分布はコーシー分布の利点である裾の長さを保ったまま、サンプリングの非効率さを解消します。例えば、
,
,
,
,
の場合には
はほぼ2となり、以下のような確率密度になります。
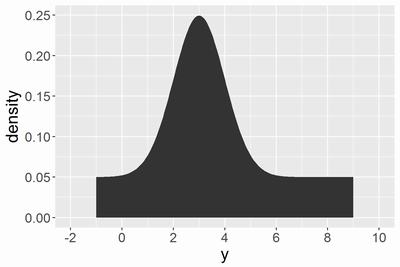
なお、Stanの計算に必要な対数尤度は以下のように式変形して表現することで高速化できます。
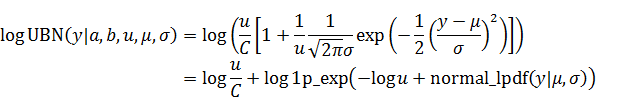
ここでlog1p_exp関数とnormal_lpdf関数は計算の高速化するためのStanの便利関数です。
2次元のスポット検出例 その1
30x30の大きさで中央部分にシグナルがあり、ノイズを加えたデータYを考えます。図にすると以下です。
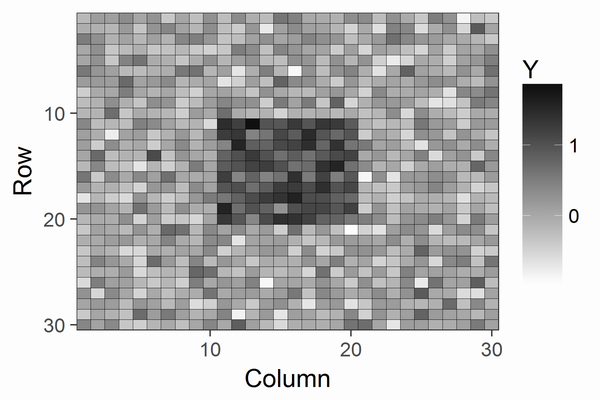
上下左右のマスとつながるマルコフ場モデルを、UBN分布を利用して実装したStanコードは以下になります。
- 5行目: 上記で説明したUBN分布の
を固定値
Uで与えています。 - 9行目:
muにノイズがのってデータYになります。設定した下限と上限がUBN分布のと
にそれぞれ対応しています。
- 17,20行目: 17行目がマルコフ場モデルの左右のつながり、20行目が上下のつながりに対応します。ここでは
Uを固定値として与えていること、またs_muの値が高々1.5ぐらいと考えられることから、UBN分布のはほぼ一定の定数です。Stanでは対数確率の偏微分が重要であり、微分で消える定数項を無視して構いません。そのため
を無視してコーディングしています。
- 21行目: ノイズをのせている部分です。状態空間モデルの観測モデルに相当します。
- 22,23行目: なくても構いませんが、変分ベイズが安定になることがあるので
s_muとs_Yに弱情報事前分布を設定しています。
このモデルは局所最適解が多くMCMCの一種であるNUTSではうまく推定できませんが、自動変分ベイズだと高速に推定できるモデルとなっています。データを生成し、推定を実行するRコードは以下になります。
- 4~9行目:データ生成部分です。
- 12行目:ここでは
Uは0.1としました。少し値を変えて実行してみて結果が頑健かチェックするとよいでしょう。
変分ベイズが高速なため、計算時間はSurface Pro 3(core i5)でも10秒以下です。推定結果は以下です。以下の図はmuの乱数サンプルの中央値を2次元でプロットした図です。
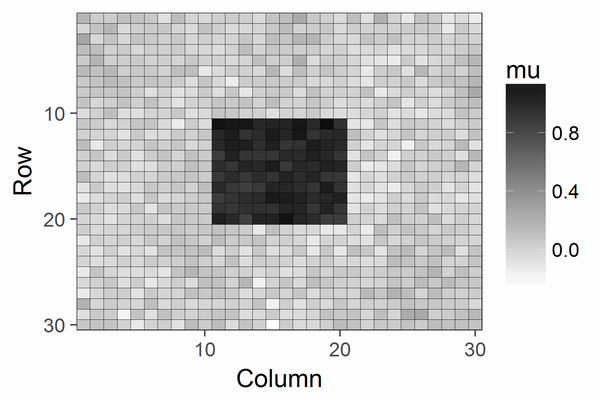
以下の図はRowの真ん中(ここでは15)に固定してスライスし、横軸をColumn・縦軸をmuにしてプロットした図です。薄い灰帯は乱数サンプルから計算した95%ベイズ信頼区間、濃い灰帯は80%ベイズ信頼区間、青線は中央値、赤線はデータです。
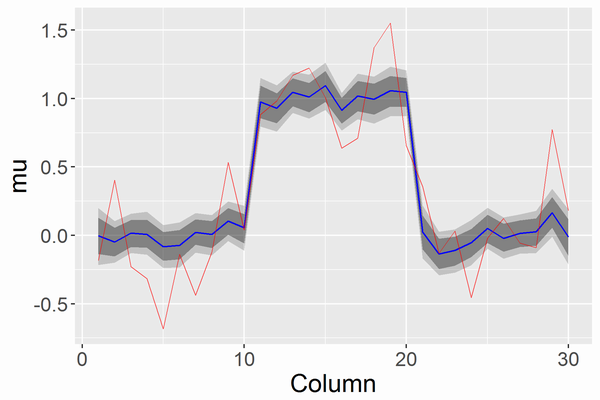
シグナルのスポットを検出できているのがわかるかと思います。上記のRコードと結果はシグナルの大きさがノイズのSDの3倍となっている場合ですが、シグナルの大きさがSDの2.5倍となっている場合の結果は以下になります。徐々にカドから崩れていきます。
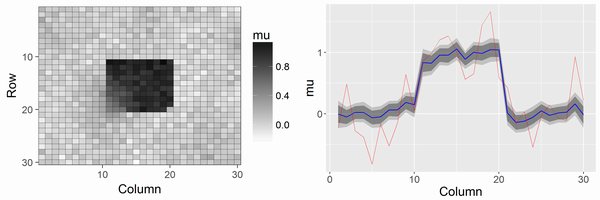
このシグナルが正方形の場合、少なくともシグナルがノイズのSDの2.3倍ぐらいないとスポットとして綺麗に検出されないようでした。
2次元のスポット検出例 その2
画素数が300x600の場合も試してみました。データ例を図にすると以下です。

モデルは同じままで、実行するRコードもほぼ同じです(データ生成部分だけわずかに異なります)。推定に要する時間は5分ぐらいでした。シグナルがノイズのSDの3倍の場合の推定結果は以下になりました。図の凡例は上記の場合と同じです。丸いスポットの検出は比較的得意ですが、尖っている箇所はやはり難しいようです。

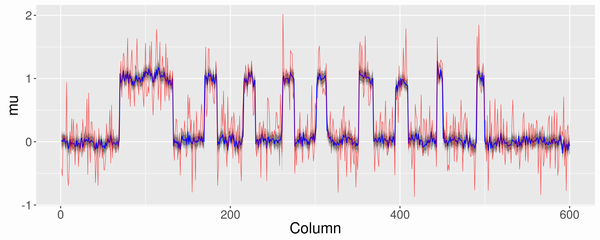
この場合、少なくともシグナルがノイズのSDの3倍ぐらいないとスポットとして綺麗に検出されないようでした。
試した範囲では、この方法によって地図上でも3次元でもスポット検出できそうです。Enjoy!